Strutinsky calculations with and without the T=1 pairing correlations

To shed more light especially on the role played by the T=1 pairing, we performed cranked Strutinsky type calculations based on a deformed WS potential. By comparing two sets of calculations, with and without the T=1 pairing, we aim at tracing the contribution and influence of the T=1 interaction. The T=1 pairing interaction is based on a seniority type force and a double stretched quadrupole interaction[29]. For the case of odd nucleon number and/or excited configurations, each configuration is blocked self-consistently[30]. The model has been successful in the description of rotational states in a wide range of nuclei.

To probe the sensitivity of our results to the macroscopic input, we performed two sets of calculations based on: (i) the Myers-Swiatecki liquid-drop (MS LD) mass formula[31] and (ii) the folded Yukawa plus exponential (FY) mass formula [32]. The MS LD mass formula can be considered as rather stiff towards deforming the nucleus. On the other hand, the FY mass formula, explicitly involving the finite range of the nuclear force and the diffuseness of the nuclear surface, results in a softer surface energy and gives larger $\beta_4$ deformations. For very light nuclei, the contribution to the surface energy can become unphysically large, but for the case of mass A=60 region, one is still on safe grounds.

In contrast to the MS LD results, for the FY mass formula all the four nuclei discussed here have T=1 paired stable minima at deformations that are comparable to those obtained without pairing, but at larger values of the hexadecapole deformation parameters. The difference in deformations between these nuclei result in distinctly different response to the rotating field. Starting with ⁵⁸Cu, we do not observe any distinct difference between the MS LD and FY calculations. Also for the case of ⁶⁰Zn, no big differences are obtained, although the crossing is somewhat sharper here in the FY case. The largest difference occurs for the case of ⁶¹Zn. Since the FY calculations yield the deformation that is larger than for ⁶⁰Zn, the neutron g_9/2 alignment is becoming more smooth, resulting in a rather modest hump in ${\cal J}^{(2)}$. In what follows we concentrate on the results of the FY calculations.

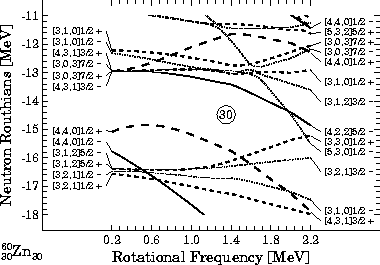
In Fig. 4 we present the WS neutron single-particle orbitals near the SD N=Z=30 magic gap in ⁶⁰Zn. Even though the HF and WS spectra presented in Figs. 1 and 4 have been calculated within so much different approaches, they present striking similarities. The equilibrium deformations of the SD shapes, calculated within the HF and Strutinsky approaches for the ⁵⁸Cu, ⁵⁹Cu, ⁶⁰Zn, and ⁶¹Zn nuclei, are presented in Table 1. The values obtained at $\hbar\omega$=0 and 1MeV illustrate the degree of the rotational polarization occurring along the SD bands. Similarly, by comparing the values for the four nuclei one can see the effects of the multipole polarizations induced by the g_9/2 protons and neutrons, cf. Refs.[16,21].

  

Figure 4: Same as in Fig. 1 but for the Woods-Saxon potential with TRS deformations $\beta_2$, $\gamma$, and $\beta_4$ calculated along the T=1 paired SD band in ⁶⁰Zn.

The LN method has been shown to be reliable for calculations of high spin states[25,26]. However, in the regime of a very weak pairing, one may encounter numerical problems in finding a proper solution. Indeed, this is the case for the present investigation, where starting from $\hbar\omega\approx$1.5MeV, the static pairing field essentially vanishes, and the pairing gaps become of the order of 100-200keV. We employ two possible schemes to avoid a numerical break down of the paired solution. Either we fix the lowest value of the gap parameter to 100-200keV, when no solution is found, or we make a transition to the non-pairing calculations. Since the calculations are done on a grid in deformation space, the frequency where the pairing solution encounters problems differs from point to point, giving fluctuations in the total energy. Changes in energy of the order of 50keV are sufficient to cause oscillations in the calculated moments of inertia. In order to address the underlying physics, therefore, we smoothed the moments of inertia in the frequency range where such oscillations occur.

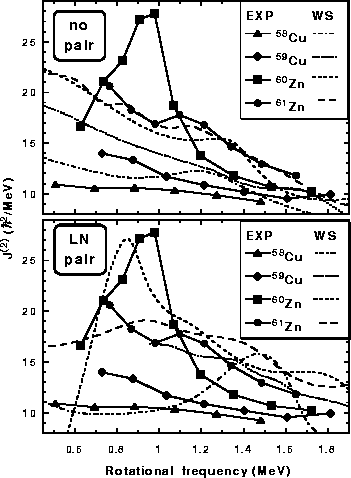
The resulting relative alignments and moments of inertia are depicted in Figs. 5 and 6, respectively. As can bee seen, the strong bump in the experimental moments of inertia of ⁶⁰Zn is rather well reproduced in the WS+LN calculations with T=1 pairing. It indeed results from the alignment of a pair of g_9/2 protons and neutrons. The crossing frequency is somewhat too small in the calculations, but this can be considered as a detail in this context. However, it might also reflect the situation in heavier nuclei, where a similar shift has been observed[5,6] and attributed to the lack of the T=0 pairing. Note that a similar behavior of ${\cal J}^{(2)}$ has been also obtained in the relativistic-mean-field LN calculations of Ref. [12], although the increase of ${\cal J}^{(2)}$ at low frequencies could not have been obtained there.

 

Table 1: Quadrupole ($\beta_2$ and $\gamma$) and hexadecapole ($\beta_4$) deformation parameters calculated for the SD configurations at $\hbar\omega$=0 and 1MeV. For each nucleus the three lines give: (a) the HF values obtained from the mass multipole moments Q₂₀, Q₂₂, and Q₄₀ through the second-order expressions for equivalent shapes[33,34], (b) the WS potential equilibrium deformations obtained by neglecting the pairing correlations, and (c) the WS potential equilibrium deformations obtained for the LN T=1 pairing. In the latter case, the $\hbar\omega$=0MeV solution in ⁵⁹Cu cannot be obtained.

		$\hbar\omega$=0MeV			$\hbar\omega$=1MeV
[1em][0em]Nucleus		$\beta_2$	$\gamma~$	$\beta_4$	$\beta_2$	$\gamma~$	$\beta_4$
[1.2em][0em]58Cu	(a)	0.371	-1$^\circ$	0.051	0.343	5$^\circ$	0.037
	(b)	0.392	0$^\circ$	0.038	0.347	7$^\circ$	0.029
	(c)	0.374	-1$^\circ$	0.061	0.357	6$^\circ$	0.024
[1.2em][0em]59Cu	(a)	0.394	0$^\circ$	0.096	0.368	3$^\circ$	0.055
	(b)	0.429	0$^\circ$	0.066	0.377	5$^\circ$	0.038
	(c)	-	-	-	0.402	3$^\circ$	0.058
[1.2em][0em]60Zn	(a)	0.412	0$^\circ$	0.144	0.391	2$^\circ$	0.089
	(b)	0.453	0$^\circ$	0.088	0.418	3$^\circ$	0.058
	(c)	0.458	4$^\circ$	0.154	0.426	2$^\circ$	0.089
[1.2em][0em]61Zn	(a)	0.428	0$^\circ$	0.143	0.410	2$^\circ$	0.098
	(b)	0.468	4$^\circ$	0.092	0.445	2$^\circ$	0.067
	(c)	0.463	-1$^\circ$	0.123	0.418	-1$^\circ$	0.085

 

The experimental moment of inertia of ⁵⁸Cu is totally flat, as one would expect since this crossing is blocked. At higher frequencies, the calculated ${\cal J}^{(2)}$ moment rises, resulting in a smaller hump centered at $\hbar\omega\approx$1.5MeV which is absent in the data. In self-consistent calculations, it is often difficult to exactly point to the cause of such apparent alignment as in the case of ⁵⁸Cu. The dominant contribution appears to come from the rather sudden drop in pairing energy, where in the region of $\hbar\omega$=1.4-1.6MeV, the pairing gap drops from a value of 0.4MeV to essentially zero. At lower frequencies, the change in pairing correlations due to the Coriolis anti-pairing is of the order of 50keV per step in $\hbar\omega$(=0.1)MeV. The sudden drop in pairing energy results in a change in the routhian $dE_{\omega}$, giving rise to this apparent alignment. Thus for all nuclei calculated in this study with the T=1 pairing, there is an excess in the moments of inertia ${\cal J}^{(2)}$ at high frequencies, most pronounced in ⁵⁸Cu. Such an excess is clearly absent in the experimental data. Since ⁵⁸Cu is taken as a reference for the relative alignment in Fig. 5b, the excess of alignment obtained in this nucleus for the T=1 paired calculations perturbs relative alignments shown for other nuclei. Another reference nucleus, e.g., ⁶⁰Zn may yield a better agreement with experiment.

  

Figure 5: Same as in Fig. 2 but for the Woods-Saxon calculations without (upper panel) and with (lower panel) pairing correlations.

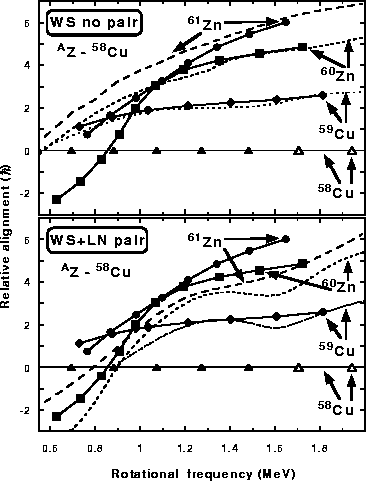For the case of ⁶¹Zn, the T=1 calculations yield minima in the TRS at large deformation, first after the alignment of the neutron g_9/2 orbits. The excess in the moments of inertia can again be traced back to the sudden drop in the pairing correlations of protons and neutrons. Before the alignment of the neutron g_9/2, the minimum is very shallow at a smaller deformation, where only a single g_9/2 orbit is occupied. In contrast, calculations without pairing yield a minimum that is stable over the entire frequency range and has a larger deformation than the one in ⁶⁰Zn. Finally, the moments of inertia of ⁵⁹Cu are rather flat, however larger than observed in experiment. Again, this is due to the decrease in the pairing energy. In ⁵⁹Cu, the TRS minimum disappears at low frequencies, and therefore the T=1 paired band cannot be followed to low spins.

  

Figure 6: Same as in Fig. 3 but for the Woods-Saxon calculations without (upper panel) and with (lower panel) pairing correlations.

Since we are dealing with nuclei that are located along the N=Zline, one may pose the question of the role of possible collective T=0 pairing and speculate a little about the influence of such correlations. As discussed elsewhere[35], the collective T=0 pairing field generally drives the nucleus to somewhat larger deformation, than when only the T=1 pair field is present. The sensitivity of our results with respect to the macroscopic model used, may point to either that the T=1 field is too strong in our calculations, or by including the T=0 field, the results would not be so sensitive to the choice of the macroscopic model. In addition, since the T=0 pair field is more resistant at high angular momenta, one may not encounter the unphysical increase in ${\cal J}^{(2)}$ that is present in the calculations based on T=1 pairing only.

At low spins, the T=0 field has essentially the same properties as the T=1, i.e., resisting the alignment of quasi-particles. Assuming that part of the correlations in our calculations are indeed due to T=0, would not affect much the case of ⁶⁰Zn, where we would see a crossing like in the calculations with T=1 (possibly shifted to somewhat larger frequencies). However, for the cases of ⁶¹Zn and ⁵⁹Cu, the blocking effect would be stronger (due to the n-p blocking), and indeed not much of the alignment would be observed (as is the case in experiment).

To really sort out these intriguing problems, unrestricted calculations need to be performed, that simultaneously take into account both T=0 and T=1 correlations. We may however already now conclude, that i) in the presence of pairing correlations, one indeed expects a hump in the moment of inertia as is observed for the case of ⁶⁰Zn and ii) the simple blocking picture does not hold here, where strong polarizing effects are present, yielding different deformation for the nuclei discussed here and as a result, different pattern of the alignment. Before such complete solutions become available, and the expectations expressed above can be corroborated, in the next section we investigate a very simple non-collective T=0 n-p pairing scenario by considering the configuration mixing of unpaired HF solutions.