Energy density at N
In this section, we apply the results obtained above to the simplest
case of spherical even-even nuclei [28], where one can
assume that the spherical symmetry, along with the space inversion
and time reversal, are simultaneously conserved symmetries.
In this case, all primary densities
![]() (23),
which we listed in Tables 3 and 4, must have
the form [39]:
(23),
which we listed in Tables 3 and 4, must have
the form [39]:
Indeed, due to the generalized Cayley-Hamilton (GCH) theorem, a
rank-![]() tensor function of a rank-
tensor function of a rank-![]() tensor must be a linear
combination of all independent rank-
tensor must be a linear
combination of all independent rank-![]() tensors built from that
rank-
tensors built from that
rank-![]() tensor, with scalar coefficients. In the GCH theorem, tensors
that differ by scalar factors are not independent.
In our case, only one
independent rank-
tensor, with scalar coefficients. In the GCH theorem, tensors
that differ by scalar factors are not independent.
In our case, only one
independent rank-![]() function
function
![]() can be built from the
rank-1 tensor (position vector
can be built from the
rank-1 tensor (position vector ![]() ), which gives
Eq. (44). The spherical symmetry assumed here is
essential for this argument to work, because many more independent
rank-
), which gives
Eq. (44). The spherical symmetry assumed here is
essential for this argument to work, because many more independent
rank-![]() tensors can be built when other ``material'' tensors (like,
e.g., the quadrupole deformation tensor) are available.
tensors can be built when other ``material'' tensors (like,
e.g., the quadrupole deformation tensor) are available.
The spherical form of
![]() (44)
requires that the following selection rule is obeyed:
(44)
requires that the following selection rule is obeyed:
In Tables 3 and 4, all densities allowed by
the conserved spherical, space-inversion, and time-reversal
symmetries are marked with bullets (![]() ). One can see that they
correspond to quantum numbers
). One can see that they
correspond to quantum numbers ![]() being equal to 000 or 202 [for
densities built from
being equal to 000 or 202 [for
densities built from
![]() ] and 111 or
313 [for densities built from
] and 111 or
313 [for densities built from
![]() ]. Then, it is easy to select
all allowed terms in the energy density--in
Tables 7-18 and 22 these are
also marked with bullets (
]. Then, it is easy to select
all allowed terms in the energy density--in
Tables 7-18 and 22 these are
also marked with bullets (![]() ). Numbers of such terms are listed in
Table 20 together with those obtained by
imposing, in addition, the Galilean or gauge invariance.
). Numbers of such terms are listed in
Table 20 together with those obtained by
imposing, in addition, the Galilean or gauge invariance.
| order | Total | Galilean | Gauge |
| 0 | 1 | 1 | 1 |
| 2 | 4 | 4 | 4 |
| 4 | 13 | 9 | 3 |
| 6 | 32 | 16 | 3 |
| N |
50 | 30 | 11 |
All results for the EDF restricted by the spherical, space-inversion,
and time-reversal symmetries can now be extracted from the general
results presented in Secs. 2 and 3 and
Appendices B and C. However, in the remainder of
this section we give an example of how these results can be
translated into those based on the Cartesian representations of
derivative operators (18)-(22). Indeed, in this
representation, all non-zero densities can be defined as:
| (57) |
The six local densities
(47)-(52)
are the Cartesian analogues of densities marked in
Table 3 with bullets (![]() ), and the four local densities
(53)-(56)
are analogues of those marked in Table 4. However, one
should note that rank-2 densities
), and the four local densities
(53)-(56)
are analogues of those marked in Table 4. However, one
should note that rank-2 densities
![]() and
and
![]() are not proportional to
are not proportional to
![]() and
and
![]() , respectively, and the rank-3 density
, respectively, and the rank-3 density
![]() is not proportional to
is not proportional to
![]() . This is so,
because they are defined in terms of the derivative operators
(18)-(22), where appropriate traces have not
been subtracted out. Nevertheless, linear relations between densities
(47)-(56)
and their spherical-representation counterparts
. This is so,
because they are defined in terms of the derivative operators
(18)-(22), where appropriate traces have not
been subtracted out. Nevertheless, linear relations between densities
(47)-(56)
and their spherical-representation counterparts
![]() can
easily be worked out and will not be presented here.
can
easily be worked out and will not be presented here.
Note also that the scalar densities ![]() and
and ![]() can be
expressed as the corresponding sums of the rank-2 densities
can be
expressed as the corresponding sums of the rank-2 densities
![]() and
and
![]() , and the vector density
, and the vector density
![]() as that of
as that of
![]() .
However, based on the results obtained in the spherical representation,
we know that they have to be treated separately to give separate
terms in the energy density.
.
However, based on the results obtained in the spherical representation,
we know that they have to be treated separately to give separate
terms in the energy density.
Again, based on the results obtained in the spherical representation,
we can write the N![]() LO energy density as a sum of contributions
from zero, second, fourth, and sixth orders:
LO energy density as a sum of contributions
from zero, second, fourth, and sixth orders:
| (58) |
| (59) |
| (60) |
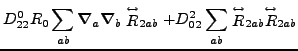 |
|||
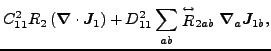 |
(61) |
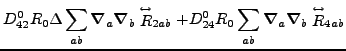 |
|||
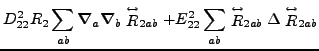 |
|||
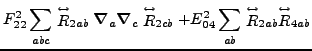 |
|||
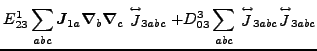 |
|||
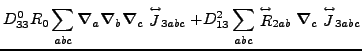 |
|||
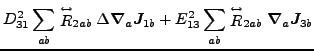 |
|||
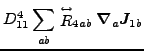 |
|||
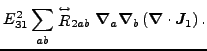 |
(62) |