When a nucleus rotates rapidly, there appear strong current and spin one-body densities along with the usual particle densities that characterize stationary (time-even) states. The time-odd densities are at the origin of strong time-odd mean fields. There are already many self-consistent studies of high-spin states available; see, e.g., reviews in Refs. [12,65,66,67]. The role and significance of the time-odd mean-field terms, however, has not been carefully studied. Basic features of high-spin states can often be well described by models that use phenomenological mean fields of the Woods-Saxon or Nilsson type, where no time-odd terms are explicitly present in the one-body potential. (The time-odd densities are, however, present there through the time-odd cranking term.) For the Gogny interaction [59], or within the standard RMF models [12], they cannot be independently modified; the Gogny interaction is defined as a two-body force (where the time-odd terms show up as exchange terms), while all time-odd terms appearing in standard RMF models are fixed by Lorentz invariance. Within the Skyrme framework, the time-odd terms in superdeformed rotational states were analyzed in an exploratory way in Refs. [3,20].
Unlike the GT response, rotational bands are influenced by both
isoscalar and isovector time-odd channels of the effective
interaction. In fact, the large effects of time-odd coupling constants
found in
[3] are mainly due to the isoscalar channel; the
isovector channel induces corrections that are smaller, though
non-negligible. The SkO' Skyrme parameterization,
which we use for GT calculations,
is unstable when the original parameters from
Eq. (34) are used in the isoscalar spin channel because
g0 < -1 (a fact that is related
to the unusually high value of g1 in Table 1).
This leads to unphysical ferromagnetic solutions where all
spins align when the nucleus is cranked.
Of course, the value of g0 does not influence the GT calculations
for even-even nuclei presented in our study which focuses on
the isovector time-odd coupling constants. Consequently, in the following
we employ a simple spin energy functional using the
Skyrme force value for C0T, setting
![]() and neglecting density dependence. We adopt the value g0 = 0.4
given in [52] (note that a different definition of the
normalization factor is used there) to fix C0s.
and neglecting density dependence. We adopt the value g0 = 0.4
given in [52] (note that a different definition of the
normalization factor is used there) to fix C0s.
We perform the calculations in exactly the same way as
in Ref. [3] by using the code HFODD (v1.75r) described
in Ref.[68]. We examine 152Dy, which is a doubly magic
superdeformed system. Pairing has a minor influence and we neglect
it. We focus on the dynamic moment of inertia ![]() :
:
![\begin{displaymath}
{\cal J}^{(2)}(I)
= \left[ \frac{d^2E}{dI^2} \right]^{-1}
\simeq \frac{4\hbar^2 }{\Delta E_\gamma}
\end{displaymath}](img161.png) |
(29) |
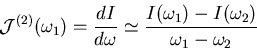 |
(30) |