Regression analysis of the GT resonances

In the previous subsection we explored the dependence of the GT resonance energies and strengths on particular time-odd coupling constants of the Skyrme functional while keeping the other coupling constants fixed. These results show that the GT properties depend on all the coupling constants simultaneously, and the effect of varying one coupling constant may be either enhanced or cancelled by a variation of another one. In such a situation, linear-regression is needed to quantify the influence of the coupling constants.

We analyze the situation by supposing that the GT energies and strengths are linear functions of four coupling constants, i.e.,

$$E^{\rm GT}_{\rm reg} \! e_0 + e_1 C_1^{s}[0] + e_2 C_1^{s}[\rho_{\rm nm}] + e_3 C_1^{\Delta s} + e_4 C_1^T ,\!\!\!$$ = (20)

$$B^{\rm GT}_{\rm reg} \! b_0 + b_1 C_1^{s}[0] + b_2 C_1^{s}[\rho_{\rm nm}] + b_3 C_1^{\Delta s} + b_4 C_1^T .\!\!\!$$ = (21)

In our linear regression method, the coefficients e_i and b_i are determined by a least-square fit of expressions (20) and (21) to the given sample of N calculated QRPA results, $E^{\rm GT}_{\rm calc}(n)$ and $B^{\rm GT}_{\rm calc}(n)$, $n=1,\ldots,N$. The calculated $B^{\rm GT}_{\rm calc}(n)$ values have been quenched by the usual factor of 1.26².

The sample of QRPA calculations covers the physically interesting range of values for the coupling constants. We present here results from a sample defined by the hypercube

$$\quad\mbox{7 values},$$ g₀' = 0.6(0.2)1.8, (22)

$$C_1^{s}[0]/C_1^{s}[\rho_{\rm nm}] = \quad\mbox{4 values},$$ -1(1)2, (23)

$$C_1^{\Delta s} = \quad\mbox{5 values},$$ -40(20)40, (24)

$$\quad\mbox{5 values},$$ C₁^T = -40(10)0, (25)

i.e., for the sample of N=700. We use g₀' instead of C₁^s[0] for the regression analysis to avoid combinations of the coupling constants that leave g₀' too far from 1.2, the value advocated in Sect. 4.3.

The left panels in Figs. 11 and 12 contain histograms of deviations

$$\delta E^{\rm GT}(n) E^{\rm GT}_{\rm calc}(n)- E^{\rm GT}_{\rm reg},$$ = (26)

$$\delta B^{\rm GT}(n) B^{\rm GT}_{\rm calc}(n)- B^{\rm GT}_{\rm reg}$$ = (27)

between the calculated and fitted energies and strengths in ¹¹²Sn, ¹²⁴Sn, and ²⁰⁸Pb. The widths of these distributions illustrate the degree to which the linear regression expressions (4.4) are able to describe the results of the QRPA calculations. One can see that the fit GT resonance energies are generally within about $\pm 1$MeV of the calculated ones, and the fit strengths within about $\pm$6.

Figure 11: Distribution of differences between calculated GT resonance energies and those from the regression analysis, with all points from the sample (left panels) and with a reduced sample (right panels).

Figure 12: Same as in Fig. 11 except for the strength in the GT resonance.

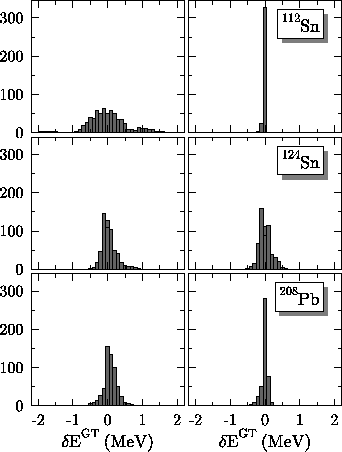As can be seen from Figs. 6, 8, 9, and 10, the dependence of both the resonance energy and the strength in the resonance on the coupling constants is not linear for the entire region of coupling constants. Although our sample is restricted to the area around the reasonable values, at times we leave the region where the regression can safely be performed. Furthermore, for certain combinations of the coupling constants (especially at a weak coupling), there are competing states that carry strength similar to that of the GT ``resonance.'' (These states often merge into the resonance at a larger coupling.) Finally, the resonance can be fragmented into many (sometimes up to 15) states. Therefore, we remove certain areas of parameter space where the determination of either the energy or the strength of the GT resonance is ambiguous. Such areas are almost always singled out by particularly large deviations from the fitted values.

After reducing the sample in this way, we obtain the histograms in the right panels of Figs. 11 and 12. These illustrate the quality of the regression fits obtained for samples of N=542, 664, and 618 in ¹¹²Sn, ¹²⁴Sn, and ²⁰⁸Pb, respectively. Tables 2 and 3 list the corresponding values of the regression coefficients, as well as the standard deviations for the GT energies and strengths within each of the samples.

Table 2: Coefficients e_i obtained by the regression analysis, Eq. (20), of the QRPA GT resonance energies in the reduced sample (see text). The standard deviations $\sigma_E$ from this sample are compared to the $\sigma_E$(full) from the full sample of N=700 points.

	112Sn	124Sn	208Pb
e0	5.58100	10.16000	8.19600
e1	0.00305	0.00488	0.00674
e2	0.02696	0.03981	0.06099
e3	0.01690	0.03474	0.05897
e4	-0.01189	-0.01767	-0.02198
$\sigma_E$	0.0479	0.199	0.114
$\sigma_E$(full)	0.585	0.865	0.520

Table 3: Same as in Table 2 except for the strengths of the GT resonances.

	112Sn	124Sn	208Pb
b0	21.86000	11.75000	80.62000
b1	0.00963	0.03107	0.03079
b2	0.06143	0.25120	0.18620
b3	0.09146	0.30510	0.33850
b4	-0.01730	-0.10280	-0.09688
$\sigma_B$	0.608	2.10	2.74
$\sigma_B$(full)	5.20	3.44	3.82

Figures 11 and 12 and the standard deviations obtained in the reduced and full samples (Tables 2 and 3) show that the description obtained by removing a small number of points beyond the region of linearity is quite good. The GT resonance energies are now reproduced within about $\pm$200keV or less. The description of the resonant GT strengths is also improved, especially in ¹¹²Sn, although here the linear regression cannot work too well because the strengths saturate at strong coupling. Nevertheless, the coefficients listed in Tables 2 and 3 allow a fairly reliable estimate of the QRPA values for any combination of the coupling constants. The values of the coefficients in Tables 2 and 3 show that $C_1^{s} [\rho _{\rm nm}]$ and $C^{\Delta s}_1$ strongly influence properties of the GT resonance, and that both the energies and the resonant strengths increase when these coupling constants increase. C^T₁ has a weaker effect in the opposite direction, while C^s₁[0] is less important still.

Without presenting detailed results, we report here on two other attempts at regression analysis. We tried to analyze the results for all the three nuclei, ¹¹²Sn, ¹²⁴Sn, and ²⁰⁸Pb, simultaneously by adding terms e₅(N-Z) and b₅(N-Z) to the regression formulas (4.4). Linear scaling might be obtained by analyzing the QRPA results for very many nuclei, where the effects due to shell structure could average out. In our small sample, shell structure is obviously important. We also tried the regression analysis with C^T₁ = -9.172MeVfm⁵ fixed at its SkO' value (see Table 4), and without the terms e₄ and b₄ in the regression formulae (4.4), so that the functional's gauge invariance was preserved. The results were not significantly different from those when C^T₁ was allowed to vary freely. Consequently, our analysis does not allow us any constraints on C^T₁ that might be used in future fits of the time-even part of the energy functional.

For the SkO' coupling constants (see Table 4), we obtain $E^{\rm GT}_{\rm reg}=8.3$MeV, 14.2MeV, and 14.2MeV in ¹¹²Sn, ¹²⁴Sn, and ²⁰⁸Pb, and $B^{\rm GT}_{\rm reg}=100$ in ²⁰⁸Pb. These values are close to the corresponding experimental data: 8.9MeV, 13.7MeV, 15.5MeV, from Ref.[46], and $\sim 3(N-Z)/1.26^2$. It is not possible, however, to find values of the four coupling constants that reproduce these four experimental data points exactly. The reason is that the matrix of corresponding regression coefficients is almost singular, resulting in absurdly large values of the coupling constants. Clearly a determination of the coupling constants from experiment would require more data. Although charge-exchange measurements have been made on many nuclei, we require spherical even-even nuclei that are not soft against vibrations. To fit the relevant coupling constants to data, we would need, at the minimum, the ability to treat deformed nuclei. Meanwhile, we can make a simple choice of time-odd coupling constants from the analysis in Fig. 6. The values

$$= C_1^s[\rho_{\rm nm}] = 120 \, {\rm MeV} \, {\rm fm}^3$$ C₁^s [0]

$$C_1^{\Delta s} \phantom{C_1^s[\rho_{\rm nm}] =} =$$ 0

$$\phantom{C_1^s[\rho_{\rm nm}] =} = -9.172 \, {\rm MeV} \, {\rm fm}^5$$ C₁^T (28)

(see Table IV) give g₀'=1.2 and g₁' = 0.19, which are in accord with the data we discuss. But these values by no means constitute a fit and are not unique.

Figure 13: Dynamical moment of inertia ${\cal J}^{(2)}$ in the superdeformed band of ¹⁵²Dy calculated with the SkO' energy density functional and modified time-odd coupling constants. In the upper left panel (corresponding to Fig. 6) all coupling constants are chosen to be density independent, $C_1^{\tau}$ is kept at the Skyrme-force value and $C_1^{\Delta s} = 0$. In the upper right panel (corresponding to Fig. 8) the density dependence of C₁^s is varied keeping g₀' = 1.2. In the lower left panel (corresponding to Fig. 9) $C_1^{\Delta s}$ is varied, while in the lower right panel (corresponding to Fig. 10) C_t^T is varied. See text for the choice of isoscalar time-odd couplings.