


Next: Energy density functional from
Up: Gamow-Teller strength and the
Previous: Summary, conclusions, and outlook
Local Densities and Currents
The complete density matrix
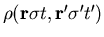 in spin-isospin space as defined in (1)
can be decomposed into the sum of scalar
in spin-isospin space as defined in (1)
can be decomposed into the sum of scalar
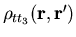 and vector densities
and vector densities
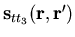 ,
where the
subscripts
denote the isospin quantum numbers:
,
where the
subscripts
denote the isospin quantum numbers:
The quantities
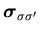 and
and
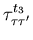 are
matrix elements of the Pauli matrices in spin and isospin space.
In terms of these, the local density
are
matrix elements of the Pauli matrices in spin and isospin space.
In terms of these, the local density 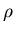 ,
spin density
,
spin density 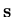 ,
kinetic density
,
kinetic density 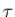 ,
kinetic spin density
,
kinetic spin density 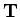 ,
current
,
current 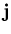 ,
and spin-orbit tensor
,
and spin-orbit tensor
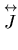 are
are
The densities 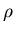 ,
,
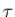 ,
and
,
and
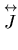 are time-even, while
are time-even, while
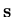 ,
,
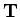 ,
and
,
and 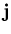 are time-odd. See [20]
for a more detailed discussion.
are time-odd. See [20]
for a more detailed discussion.



Next: Energy density functional from
Up: Gamow-Teller strength and the
Previous: Summary, conclusions, and outlook
Jacek Dobaczewski
2002-03-15
![$\displaystyle + \delta_{\sigma \sigma'} \! \sum_{t_3 = -1}^{+1}
\rho_{1 t_3} (\...
...dot \mbox{{\boldmath {$\sigma$}}}_{\sigma \sigma'}
\tau^{t_3}_{\tau\tau'}
\Big]$](img168.png)
![$\displaystyle + \delta_{\sigma \sigma'} \! \sum_{t_3 = -1}^{+1}
\rho_{1 t_3} (\...
...dot \mbox{{\boldmath {$\sigma$}}}_{\sigma \sigma'}
\tau^{t_3}_{\tau\tau'}
\Big]$](img168.png)