


Next: The Skyrme energy functional
Up: A generalized Skyrme energy
Previous: A generalized Skyrme energy
Many calculations performed with the Skyrme interaction can be viewed as
energy-density theory in the spirit of the Hohenberg-Kohn-Sham
approach [15], originally introduced for many-electron
systems. Nowadays, energy density theory is a standard tool in atomic,
molecular, cluster, and solid-state physics [16], as well
as in nuclear physics [17]. The starting point is an energy
functional 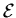 of all local densities and currents
of all local densities and currents 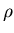 ,
,
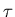 ,
,
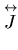 ,
,
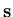 ,
,
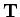 ,
and
,
and 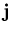 that can
be constructed from the most general single-particle density matrix
that can
be constructed from the most general single-particle density matrix
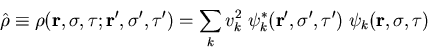 |
(1) |
(see Appendix 7 for more details), where 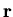 ,
,
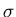 ,
and t are the spatial, spin, and isospin coordinates of the
wave function. The Hohenberg-Kohn-Sham approach maps the nuclear
many-body problem for the ``real'' highly correlated many-body wave
function on a system of independent particles in so-called Kohn-Sham
orbitals
,
and t are the spatial, spin, and isospin coordinates of the
wave function. The Hohenberg-Kohn-Sham approach maps the nuclear
many-body problem for the ``real'' highly correlated many-body wave
function on a system of independent particles in so-called Kohn-Sham
orbitals 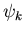 .
The equations of motion for
.
The equations of motion for 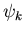 are derived
from the variational principle
are derived
from the variational principle
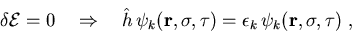 |
(2) |
where the single-particle Hamiltonian 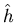 is the sum of the
kinetic term
is the sum of the
kinetic term 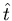 and the self-consistent potential
and the self-consistent potential 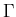 that is calculated from the density matrix
that is calculated from the density matrix
![\begin{displaymath}
\hat{h}
= \frac{\delta {\cal E}}{\delta \hat\rho}
= \hat{t} + \hat\Gamma [\hat\rho]
\quad .
\end{displaymath}](img19.png) |
(3) |
The existence theorem for the effective energy functional makes no
statement about its structure. The theoretical challenge is to find an
energy functional that incorporates all relevant physics with as few
free parameters as possible. The density functional approach as used
here is equivalent to the local density approximation to the
nuclear G matrix [18].
The energy functional investigated here in detail describes the
particle-hole channel of the effective interaction only.
For the treatment of pairing correlations, the energy functional has
to be complemented by an effective particle-particle interaction
that is constructed in a similar way from the pairing density matrix;
see [19] for details. We use here the simplest functional
proportional to the square of the local pair density with the
coupling constants given in [11].



Next: The Skyrme energy functional
Up: A generalized Skyrme energy
Previous: A generalized Skyrme energy
Jacek Dobaczewski
2002-03-15
![\begin{displaymath}
\hat{h}
= \frac{\delta {\cal E}}{\delta \hat\rho}
= \hat{t} + \hat\Gamma [\hat\rho]
\quad .
\end{displaymath}](img19.png)