


Next: Existing parameterizations
Up: A generalized Skyrme energy
Previous: Basics of energy density
Within the local-density approximation, the energy functional is given
by the spatial integral of the local energy density
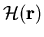
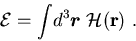 |
(4) |
The energy density is composed of the kinetic term
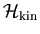 ,
the Skyrme energy density
,
the Skyrme energy density
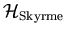 that describes the
effective strong interaction between the nucleons, and a term arising
from the
electromagnetic interaction
that describes the
effective strong interaction between the nucleons, and a term arising
from the
electromagnetic interaction
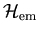 :
:
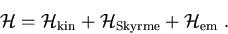 |
(5) |
For the electromagnetic interaction, we take the standard Coulomb
expression,
including the Slater approximation for the exchange
term. The energy functional discussed here contains all possible
terms bilinear in local densities and currents and up to second order
in the derivatives that are invariant under reflection,
time-reversal, rotation, translation, and isospin rotation
[20].
Time-reversal invariance requires the energy density
to be bilinear in either time-even densities or time-odd densities,
so the Skyrme energy density can be separated into a ``time-even"
part
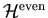 and a ``time-odd" part
and a ``time-odd" part
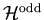 :
:
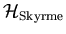 |
= |
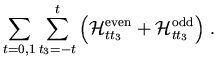 |
(6) |
The sum runs over the isospin t and its third component t3.
Only the t3 = 0 component of the isovector t = 1
terms contribute to nuclear ground states and the rotational bands
discussed later, while the 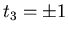 components contribute
only to charge-exchange (e.g. GT) excitations. In the notation of
Refs. [3,20],
the time-even and time-odd Skyrme energy densities read
components contribute
only to charge-exchange (e.g. GT) excitations. In the notation of
Refs. [3,20],
the time-even and time-odd Skyrme energy densities read
Isospin invariance of the Skyrme interaction makes the coupling
constants independent of the isospin z-projection.
All coupling constants might be density dependent. Following the
standard ansatz for the Skyrme interaction, we neglect such a
possibility
except in 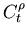 and Cts, for which we restrict the density
dependence to the following form
and Cts, for which we restrict the density
dependence to the following form
Here 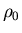 is the isoscalar scalar density, and
is the isoscalar scalar density, and 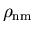 is its
value in saturated infinite nuclear matter. The exponent
is its
value in saturated infinite nuclear matter. The exponent 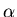 that
specifies the density dependence of
that
specifies the density dependence of
![$C_t^{\rho} [\rho_0]$](img45.png) must be
about 0.25 for the incompressibility coefficient
must be
about 0.25 for the incompressibility coefficient 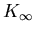 to be
correct[21,22,23,24]. Although this fact does
not restrict the analogous power in
to be
correct[21,22,23,24]. Although this fact does
not restrict the analogous power in
![$C_t^{s} [\rho_0]$](img47.png) ,
Eq. (10), we keep
,
Eq. (10), we keep 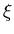 equal to
equal to 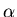 for simplicity here.
Usually we will consider energy functionals that
are invariant under local gauge transformations [3], which
generalize the Galilean invariance of the Skyrme interaction discussed
in
[2]. Gauge invariance links three pairs of time-even and
time-odd terms in the energy functional:
for simplicity here.
Usually we will consider energy functionals that
are invariant under local gauge transformations [3], which
generalize the Galilean invariance of the Skyrme interaction discussed
in
[2]. Gauge invariance links three pairs of time-even and
time-odd terms in the energy functional:
| Ctj |
= |
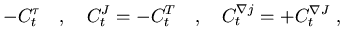 |
(11) |
These relations fix all orbital time-odd terms, leaving only
time-odd terms corresponding to the spin-spin interaction with free
coupling constants. Relations (11) lead to a simplified
form of Eqs. (6)-(8),
The time-even terms of the energy functional can be directly
related to nuclear bulk properties such as E/A, the saturation density
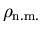 ,
incompressibility, symmetry energy, surface and
surface symmetry energy, and spin-orbit splittings. The remaining
time-odd terms cannot.
,
incompressibility, symmetry energy, surface and
surface symmetry energy, and spin-orbit splittings. The remaining
time-odd terms cannot.
We will set the coupling constant
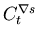 to 0. The term it multiplies comes
from a local two-body tensor force considered in Skyrme's original
papers [25] and discussed by Stancu et al. [26],
but omitted in all modern Skyrme parameterizations except the force SL1
introduced by Liu et al. [27], which has not been used since.
to 0. The term it multiplies comes
from a local two-body tensor force considered in Skyrme's original
papers [25] and discussed by Stancu et al. [26],
but omitted in all modern Skyrme parameterizations except the force SL1
introduced by Liu et al. [27], which has not been used since.



Next: Existing parameterizations
Up: A generalized Skyrme energy
Previous: Basics of energy density
Jacek Dobaczewski
2002-03-15
![]() and a ``time-odd" part
and a ``time-odd" part
![]() :
:
![]() to 0. The term it multiplies comes
from a local two-body tensor force considered in Skyrme's original
papers [25] and discussed by Stancu et al. [26],
but omitted in all modern Skyrme parameterizations except the force SL1
introduced by Liu et al. [27], which has not been used since.
to 0. The term it multiplies comes
from a local two-body tensor force considered in Skyrme's original
papers [25] and discussed by Stancu et al. [26],
but omitted in all modern Skyrme parameterizations except the force SL1
introduced by Liu et al. [27], which has not been used since.