In the mean-field approximation,
![]() ,
the
density of particles in momentum space with the isospin projection q
and spin projection
,
the
density of particles in momentum space with the isospin projection q
and spin projection ![]() ,
is
,
is
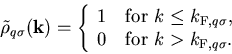 |
(36) |
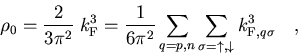 |
(37) |
| (38) |
| (39) |
| = | |||
| = | |||
| T0 | = | ||
| T1 | = | (40) |
| Fm(0) | = | ||
| = | |||
| = | |||
| = | |||
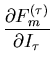 |
= | 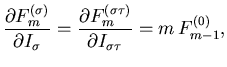 |
|
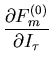 |
= | 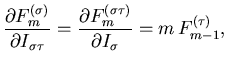 |
|
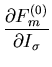 |
= | 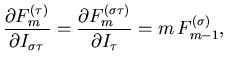 |
|
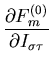 |
= | 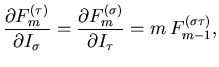 |
(41) |
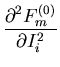 |
= | ||
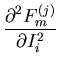 |
= | (42) |
| F0(0) | = | ||
| F1(0) | = | (43) |
| Fm(0)(0,0,0) | = | ||
| Fm(0)(1,0,0) | = | Fm(0)(0,1,0) = Fm(0)(0,0,1) = 2m-1 | |
| = | |||
| Fm(0)(1,1,1) | = | (44) |