


Next: Pressure, Incompressibility and Asymmetry
Up: Infinite Nuclear Matter
Previous: Fermi surfaces and kinetic
In INM
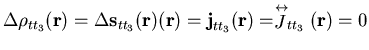 .
We choose pure neutron and proton states, which leads to
.
We choose pure neutron and proton states, which leads to
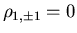 ,
,
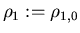 ,
and similarly for all
other densities. We take the z axis as the quantization axis for
the spin, i.e.,
st, x = st, y = 0,
st := st, z, and for
the kinetic spin density
,
and similarly for all
other densities. We take the z axis as the quantization axis for
the spin, i.e.,
st, x = st, y = 0,
st := st, z, and for
the kinetic spin density 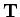 .
As discussed in Refs. [72],
this breaks the isotropy of INM, leading to an axially deformed Fermi
surface, an effect which we neglect. Adding the kinetic term, the total
energy per nucleon (i.e. the ``equation of state'') for the energy
functional (7) and (8) is given by
.
As discussed in Refs. [72],
this breaks the isotropy of INM, leading to an axially deformed Fermi
surface, an effect which we neglect. Adding the kinetic term, the total
energy per nucleon (i.e. the ``equation of state'') for the energy
functional (7) and (8) is given by
For unpolarized INM one has
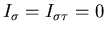 which
recovers the expression given in Ref.[23].
which
recovers the expression given in Ref.[23].
An interesting special case is polarized neutron matter, which
is discussed in [70] for the Skyrme interactions. A stability
criterion derived there from the two-body force point of view
as outlined in Appendix 8 was used to constrain
the parameters of the
SLyx forces [23,24]. In this limiting case, one has
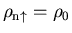 ,
,
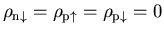 ,
which is equivalent
to
,
which is equivalent
to
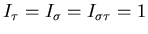 and leads to
and leads to
Expressions (34) for an antisymmetrized Skyrme force imply that
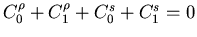 ,
and
,
and
![\begin{displaymath}
\frac{{\cal H}}{\rho_0}
= 2^{4/3} \beta {\textstyle\frac{{3...
...} \, t_2 \, (1 + x_2) \, \rho_0
\right]
\rho_0^{2/3}
\quad .
\end{displaymath}](img311.png) |
(47) |
The stability of polarized neutron matter for all densities requires
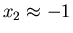 [70], so the SLyx interactions take
[70], so the SLyx interactions take
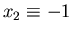 [23,24]. However, from the energy-density-functional
point of view, the coupling constants are independent, and the second
term in Eq. (50) also contributes to the
stability condition.
[23,24]. However, from the energy-density-functional
point of view, the coupling constants are independent, and the second
term in Eq. (50) also contributes to the
stability condition.



Next: Pressure, Incompressibility and Asymmetry
Up: Infinite Nuclear Matter
Previous: Fermi surfaces and kinetic
Jacek Dobaczewski
2002-03-15
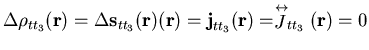 .
We choose pure neutron and proton states, which leads to
.
We choose pure neutron and proton states, which leads to
![]() ,
,
![]() ,
which is equivalent
to
,
which is equivalent
to
![]() and leads to
and leads to