Effective Interactions (II)

To a certain extent, a way out from the explosion of dimensionality, discussed in Sec. 4.1, may consist in using a better single-particle space. Instead of parametrizing fields $a^+_x$ by space-spin-isospin points $x$, one can use a parametrization by the shell-model orbitals $\phi_{i}(x)$ that are active near the Fermi surface of a given nucleus, i.e., by fields

$$a^+_i = \int\hspace{-1.2em}\sum {\rm d}{x}\,\phi_{i}(x) a^+_x .$$ (64)

When a complete set of orbitals is used, the descriptions in terms of creation operators $a^+_i$ and $a^+_x$ are equivalent. However, one can also attempt a drastic reduction of the set $a^+_i$ to a finite number, $i$=1...$M$, of ``most important'' orbitals, similarly as we have been previously using finite sets of the space-spin-isospin points instead of continuous variables.

The reduction is now not a mere question of discretizing continuous fields, but involves a serious limitation of the Hilbert space. In quantum mechanics one can always split the Hilbert space into two subspaces, $\vert\Psi\rangle=P\vert\Psi\rangle+Q\vert\Psi\rangle$, where $P$ and $Q$ are projection operators such that $P+Q=1$. Then, the Schrödinger equation $H\vert\Psi\rangle$=$E\vert\Psi\rangle$ is strictly equivalent to the following 2$\times$2 matrix of equations,

$$\left(\begin{array}{cc} PHP & PHQ \\ QHP & QHQ \end{array}\r... ...ert\Psi\rangle \\ Q\vert\Psi\rangle \end{array}\right) \quad .$$ (65)

Using the second equation, one can now formally express the ``excluded'' component, $\vert\Psi_Q\rangle$$\equiv$$Q\vert\Psi\rangle$, of the wave function by the ``kept'' component, $\vert\Psi_P\rangle$$\equiv$$P\vert\Psi\rangle$, i.e.,

$$\vert\Psi_Q\rangle = \frac{1}{E-QH}\,QH\vert\Psi_P\rangle,$$ (66)

and put it back into the first equation. This gives the Schrödinger equation reduced to the ``kept'' Hilbert space,

$$H_{\mbox{\scriptsize {eff}}}\vert\Psi_P\rangle = E\vert\Psi_P\rangle,$$ (67)

where the effective Hamiltonian $H_{\mbox{\scriptsize {eff}}}$ is given by the Bloch-Horowitz equation Blo58,

$$H_{\mbox{\scriptsize {eff}}} = H + H\,\frac{1}{E-QH}\,QH \quad .$$ (68)

The main questions is, of course, whether the Bloch-Horowitz effective interaction, $V_{\mbox{\scriptsize {eff}}}$= $H_{\mbox{\scriptsize {eff}}}-T$, can be replaced by a simple phenomenological interaction, and used to describe real systems. In particular, when a two-body, energy-independent interaction is postulated in a very small phase space, one obtains the shell model, which is successfully used since many years in nuclear structure physics.

Figure 9: Dimension of the shell-model space for calculations of $N$=$Z$ nuclei within the $pf$ space. (Picture courtesy: W. Nazarewicz, ORNL/University of Tennessee/Warsaw University.) From http://www-highspin.phys.utk.edu/~ witek/.

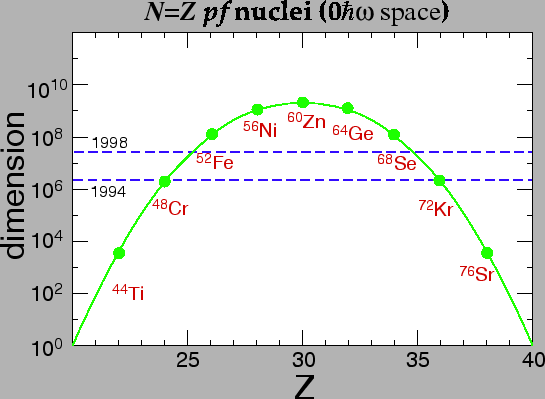In order to illustrate the dimensions of the shell-model Hilbert space, in Fig. 9 we show the numbers of many-fermion states that are obtained when states in $N$=$Z$ medium heavy nuclei are described within the $pf$ space (20 s.p. states for protons and 20 for neutrons). Currently, complete solutions for the $pf$ space become available, i.e., dimensions of the order of 10$^9$ can effectively be treated. Progress in this domain closely follows the progress in size and speed of computers, i.e., one order of magnitude is gained in about every two-three years. We shell not discuss these methods in any more detail, because dedicated lectures have been presented on this subject during the Summer School.