


Next: Local Density Approximation
Up: MANY-NUCLEON SYSTEMS
Previous: Hartree-Fock method
Conserved and Broken Symmetries
Representation of many-fermion states by density matrices
(59) and (60), and the HF approximation of the
two-body density matrix (69), allow us to give a precise
definition of what one really means by conserved and broken
symmetries in many-body systems. Moreover, it also links the
spontaneous symmetry breaking mechanism to a description
of correlations.
Consider a unitary symmetry operator 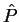 such that
such that
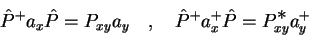 |
(76) |
and
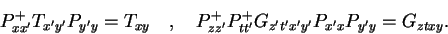 |
(77) |
Equations (76) and (77) are equivalent to the
symmetry condition
![$[\hat{H},\hat{P}]$](img378.png) =0 obeyed by Hamiltonian
(57). Symmetry operator
=0 obeyed by Hamiltonian
(57). Symmetry operator 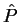 acts in the fermion
Fock space by mixing elementary fields
acts in the fermion
Fock space by mixing elementary fields 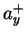 with the integral
kernel
with the integral
kernel 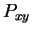 (remember that the sum-integral
(remember that the sum-integral
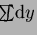 is implied for every repeated index). All the most interesting
symmetries act in this way - they can be represented as exponents of
one-body symmetry generators, i.e.,
is implied for every repeated index). All the most interesting
symmetries act in this way - they can be represented as exponents of
one-body symmetry generators, i.e., 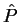 can be any one of the
following:
can be any one of the
following:
- 1�egintex2html_wrap_inlinecircendtex2html_wrap_inline.
- translational symmetry,
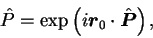 |
(78) |
where
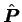 =
=
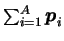 is the total linear
momentum operator, and
is the total linear
momentum operator, and
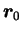 is the shift vector.
is the shift vector.
- 2�egintex2html_wrap_inlinecircendtex2html_wrap_inline.
- rotational symmetry,
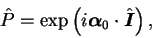 |
(79) |
where
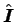 =
=
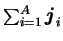 is the total angular
momentum operator, and
is the total angular
momentum operator, and
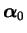 is the rotation angle.
is the rotation angle.
- 3�egintex2html_wrap_inlinecircendtex2html_wrap_inline.
- isospin symmetry,
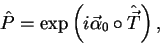 |
(80) |
where 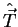 =
=
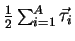 is the total isospin
operator, and
is the total isospin
operator, and
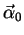 is the iso-rotation angle.
is the iso-rotation angle.
- 4�egintex2html_wrap_inlinecircendtex2html_wrap_inline.
- particle-number symmetry,
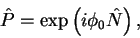 |
(81) |
where 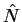 =
=
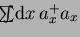 is the total particle number
operator, and
is the total particle number
operator, and 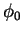 is the gauge angle.
is the gauge angle.
- 5�egintex2html_wrap_inlinecircendtex2html_wrap_inline.
- inversion (parity) symmetry,
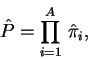 |
(82) |
where 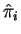 is the inversion operator for the
is the inversion operator for the  th particle.
th particle.
- 6�egintex2html_wrap_inlinecircendtex2html_wrap_inline.
- time-reversal symmetry.
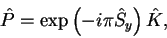 |
(83) |
where 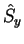 =
=
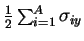 is the
is the 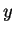 component of the total spin operator, and
component of the total spin operator, and 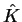 is the
complex conjugation operator in spatial representation.
is the
complex conjugation operator in spatial representation.
There can also be terms in the Hamiltonian that explicitly
break some of the above symmetries (e.g., the Coulomb interaction
explicitly breaks the isospin symmetry), but we disregard them for
simplicity.
Let us begin with the simplest case, namely, let 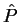 be the
parity symmetry (82). In this case, the integral kernel
reads
be the
parity symmetry (82). In this case, the integral kernel
reads 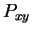
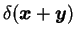 , and is, of course,
independent of spin and isospin. For a parity-invariant interaction,
Eq. (77), the exact energy of an arbitrary state
, and is, of course,
independent of spin and isospin. For a parity-invariant interaction,
Eq. (77), the exact energy of an arbitrary state
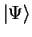 , Eq. (58), depends only on the scalar parts
(in this case, the parity invariant parts) of the one- and two-body
density matrices, i.e.,
, Eq. (58), depends only on the scalar parts
(in this case, the parity invariant parts) of the one- and two-body
density matrices, i.e.,
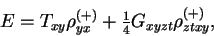 |
(84) |
for
Within the HF approximation (69), we may have two classes
of solutions:
- symmetry-conserving solution:
- symmetry-breaking solution:
In the case of the broken symmetry, neither of the density matrices is
invariant with respect to the symmetry operator. However, the
symmetry breaking part of the one-body density matrix
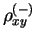 enters the HF energy (84) only through
the two-body interaction energy. Moreover, the symmetry-projected
two-body density matrix (90) does not obey the HF
condition (69). In other words, the symmetry-breaking part
of the one-body density matrix gives a correlation term of the
two-body density matrix. Symmetry breaking is, therefore, a
reflection of correlations beyond HF, taken into account with respect
to the symmetry-conserving HF method.
enters the HF energy (84) only through
the two-body interaction energy. Moreover, the symmetry-projected
two-body density matrix (90) does not obey the HF
condition (69). In other words, the symmetry-breaking part
of the one-body density matrix gives a correlation term of the
two-body density matrix. Symmetry breaking is, therefore, a
reflection of correlations beyond HF, taken into account with respect
to the symmetry-conserving HF method.
One can also say that the symmetry-breaking part
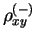 constitutes an additional set of variational parameters, which become
allowed when a larger class of the one-body density matrices (beyond
symmetry conservation) is considered. As in every variational
procedure, a larger variational class may lead (sometimes) to lower
energies. Whether it does, depends on the specific case, and in
particular on the type of the two-body interaction. It is obvious,
that one can gain energy by breaking symmetry only if the appropriate
correlation energy is negative, i.e., when the last two terms of the
two-body density matrix,
constitutes an additional set of variational parameters, which become
allowed when a larger class of the one-body density matrices (beyond
symmetry conservation) is considered. As in every variational
procedure, a larger variational class may lead (sometimes) to lower
energies. Whether it does, depends on the specific case, and in
particular on the type of the two-body interaction. It is obvious,
that one can gain energy by breaking symmetry only if the appropriate
correlation energy is negative, i.e., when the last two terms of the
two-body density matrix,
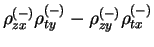 , give a negative contribution when
averaged with the two-body effective interaction
, give a negative contribution when
averaged with the two-body effective interaction  .
.
Within such an approach to the symmetry breaking, one does not, in
fact, break any symmetry of the exact wave function. Indeed, the
density matrices,
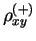 and
and
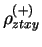 that are
``active'' in the total energy do conserve the symmetry. We should
also use these density matrices to calculate all other observables
for the symmetry-broken (correlated) solution of the HF equations.
that are
``active'' in the total energy do conserve the symmetry. We should
also use these density matrices to calculate all other observables
for the symmetry-broken (correlated) solution of the HF equations.
Let us now give results of an analogous analysis for the case of
deformed nuclei, i.e., for the case of broken rotational
symmetry (79). For axial shapes we then have the
following density matrices,
and the total HF energy,
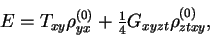 |
(93) |
that depends only on the scalar (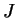 =0) parts of the density matrices.
On the other hand, the broken-symmetry one-body density matrix is the
sum of components
=0) parts of the density matrices.
On the other hand, the broken-symmetry one-body density matrix is the
sum of components
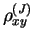 that transform as irreducible
rotational tensors of rank
that transform as irreducible
rotational tensors of rank 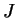 . In the scalar two-body density matrix
(92), these components are coupled to
. In the scalar two-body density matrix
(92), these components are coupled to 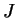 =0, and every such
a term defines the multipole correlation energy of rank
=0, and every such
a term defines the multipole correlation energy of rank 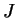 . It is
now obvious that the broken-symmetry solution becomes the ground
state for interactions that have appropriately strong
multipole-multipole terms (see Refs. Dob88,Wer94 for
numerical results in heavy nuclei).
. It is
now obvious that the broken-symmetry solution becomes the ground
state for interactions that have appropriately strong
multipole-multipole terms (see Refs. Dob88,Wer94 for
numerical results in heavy nuclei).
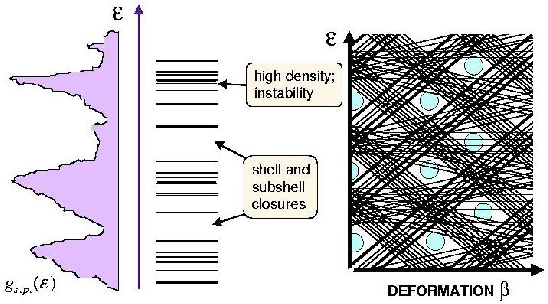
Figure 10:
Schematic illustration of the s.p. level density (left),
corresponding to the s.p. spectrum of a deformed nucleus (centre).
The right panel shows the evolution of the spectrum with nuclear
deformation.
(Picture courtesy: W. Nazarewicz,
ORNL/University of Tennessee/Warsaw University.)
From http://www-highspin.phys.utk.edu/~ witek/.
 |
Without going into detailed discussion of the multipole-multipole
decomposition of effective interactions, we may easily tell in which
nuclei the rotational symmetry is broken and deformation appears. A
schematic diagram presented in the right panel of Fig. 10
shows the evolution of the s.p. spectrum with nuclear deformation,
i.e., the dependence of eigenvalues of the mean-field Hamiltonian
having the shape characterized by the deformation parameter 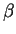 .
In such a spectrum, some s.p. levels go down, and other go up in
energy, and at specific deformations there appear in the spectrum
larger or smaller gaps. When the particles are filling the lowest
levels up to certain energy (prescribed by the number of
particles), the last occupied level may appear either below or above
the gap. This leads respectively to a decrease or an increase of the
total energy. The overall density of s.p. levels at the Fermi
surface determines, therefore, the total energy of the system. In
other words, a system having a given number of particles adopts the
shape at which the last occupied level is below a large gap.
Therefore, nuclei that correspond to magic particle numbers are
spherical (large gaps appear at spherical shape) and the rotational
symmetry is conserved, while nuclei with particle numbers between
the magic gaps (the so-called open-shell nuclei) choose non-zero deformed
ground states corresponding to broken rotational symmetry.
.
In such a spectrum, some s.p. levels go down, and other go up in
energy, and at specific deformations there appear in the spectrum
larger or smaller gaps. When the particles are filling the lowest
levels up to certain energy (prescribed by the number of
particles), the last occupied level may appear either below or above
the gap. This leads respectively to a decrease or an increase of the
total energy. The overall density of s.p. levels at the Fermi
surface determines, therefore, the total energy of the system. In
other words, a system having a given number of particles adopts the
shape at which the last occupied level is below a large gap.
Therefore, nuclei that correspond to magic particle numbers are
spherical (large gaps appear at spherical shape) and the rotational
symmetry is conserved, while nuclei with particle numbers between
the magic gaps (the so-called open-shell nuclei) choose non-zero deformed
ground states corresponding to broken rotational symmetry.



Next: Local Density Approximation
Up: MANY-NUCLEON SYSTEMS
Previous: Hartree-Fock method
Jacek Dobaczewski
2003-01-27
![]() such that
such that
![]() be the
parity symmetry (82). In this case, the integral kernel
reads
be the
parity symmetry (82). In this case, the integral kernel
reads ![]()
![]()
![]() , and is, of course,
independent of spin and isospin. For a parity-invariant interaction,
Eq. (77), the exact energy of an arbitrary state
, and is, of course,
independent of spin and isospin. For a parity-invariant interaction,
Eq. (77), the exact energy of an arbitrary state
![]() , Eq. (58), depends only on the scalar parts
(in this case, the parity invariant parts) of the one- and two-body
density matrices, i.e.,
, Eq. (58), depends only on the scalar parts
(in this case, the parity invariant parts) of the one- and two-body
density matrices, i.e.,
![]() constitutes an additional set of variational parameters, which become
allowed when a larger class of the one-body density matrices (beyond
symmetry conservation) is considered. As in every variational
procedure, a larger variational class may lead (sometimes) to lower
energies. Whether it does, depends on the specific case, and in
particular on the type of the two-body interaction. It is obvious,
that one can gain energy by breaking symmetry only if the appropriate
correlation energy is negative, i.e., when the last two terms of the
two-body density matrix,
constitutes an additional set of variational parameters, which become
allowed when a larger class of the one-body density matrices (beyond
symmetry conservation) is considered. As in every variational
procedure, a larger variational class may lead (sometimes) to lower
energies. Whether it does, depends on the specific case, and in
particular on the type of the two-body interaction. It is obvious,
that one can gain energy by breaking symmetry only if the appropriate
correlation energy is negative, i.e., when the last two terms of the
two-body density matrix,
![]() , give a negative contribution when
averaged with the two-body effective interaction
, give a negative contribution when
averaged with the two-body effective interaction ![]() .
.
![]() and
and
![]() that are
``active'' in the total energy do conserve the symmetry. We should
also use these density matrices to calculate all other observables
for the symmetry-broken (correlated) solution of the HF equations.
that are
``active'' in the total energy do conserve the symmetry. We should
also use these density matrices to calculate all other observables
for the symmetry-broken (correlated) solution of the HF equations.

![]() .
In such a spectrum, some s.p. levels go down, and other go up in
energy, and at specific deformations there appear in the spectrum
larger or smaller gaps. When the particles are filling the lowest
levels up to certain energy (prescribed by the number of
particles), the last occupied level may appear either below or above
the gap. This leads respectively to a decrease or an increase of the
total energy. The overall density of s.p. levels at the Fermi
surface determines, therefore, the total energy of the system. In
other words, a system having a given number of particles adopts the
shape at which the last occupied level is below a large gap.
Therefore, nuclei that correspond to magic particle numbers are
spherical (large gaps appear at spherical shape) and the rotational
symmetry is conserved, while nuclei with particle numbers between
the magic gaps (the so-called open-shell nuclei) choose non-zero deformed
ground states corresponding to broken rotational symmetry.
.
In such a spectrum, some s.p. levels go down, and other go up in
energy, and at specific deformations there appear in the spectrum
larger or smaller gaps. When the particles are filling the lowest
levels up to certain energy (prescribed by the number of
particles), the last occupied level may appear either below or above
the gap. This leads respectively to a decrease or an increase of the
total energy. The overall density of s.p. levels at the Fermi
surface determines, therefore, the total energy of the system. In
other words, a system having a given number of particles adopts the
shape at which the last occupied level is below a large gap.
Therefore, nuclei that correspond to magic particle numbers are
spherical (large gaps appear at spherical shape) and the rotational
symmetry is conserved, while nuclei with particle numbers between
the magic gaps (the so-called open-shell nuclei) choose non-zero deformed
ground states corresponding to broken rotational symmetry.