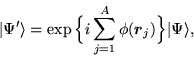Next: Skyrme interaction energy functional
Up: The Energy Density Functional
Previous: The Energy Density Functional
Local gauge invariance
Under a local gauge transformation [175], many body
wave function is multiplied by position-dependent phase factor
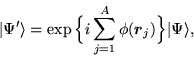 |
(82) |
which induces the following gauge transformations of density matrices
(1) and (4),
The Galilean transformation is a local gauge transformation for
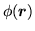 =
=
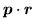 , where
, where
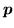 is a constant boost momentum. In analogy to that, one can introduce
the local momentum field defined by
is a constant boost momentum. In analogy to that, one can introduce
the local momentum field defined by
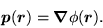 |
(85) |
Local and momentum-independent interaction is invariant with respect
to local gauge transformation, and hence energy densities
(78) and (80) must then also be independent of the
local gauge. The question whether it is possible to model nuclear
effective interactions in the p-h and p-p channels by
a local and momentum-independent interaction, is open. Therefore,
gauge transformation of the energy density can, in principle, be
respected or not, depending on a choice of dynamics one makes.
It is easy to tell when the local energy densities (78)
and (80) are local-gauge invariant, because properties of
local densities (38)-(50) under gauge
transformation read explicitly
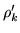 |
 |
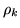 |
(86) |
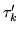 |
 |
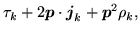 |
(87) |
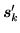 |
 |
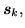 |
(88) |
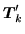 |
 |
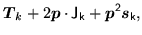 |
(89) |
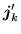 |
 |
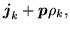 |
(90) |
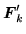 |
 |
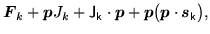 |
(91) |
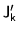 |
 |
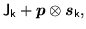 |
(92) |
where 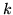 =0,1,2,3, and
=0,1,2,3, and
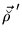 |
 |
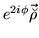 |
(93) |
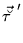 |
 |
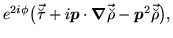 |
(94) |
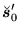 |
 |
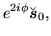 |
(95) |
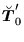 |
 |
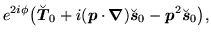 |
(96) |
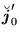 |
 |
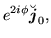 |
(97) |
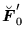 |
 |
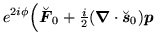 |
|
| |
|
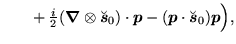 |
(98) |
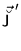 |
 |
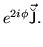 |
(99) |
Since all local p-p densities (93) are
multiplied under the gauge transformation by phase factors
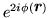 , products of local p-p densities are
not gauge invariant. Therefore, all terms not shown explicitly in
the p-p energy density [see discussion below Eq. (80)] violate the gauge invariance. On the other hand,
products of complex conjugate p-p densities and p-p
densities may be gauge invariant. This obviously is the case for
the pairing, spin, current, and spin-current p-p densities,
while only specific combinations of kinetic, spin-kinetic, and
tensor-kinetic densities are gauge invariant.
, products of local p-p densities are
not gauge invariant. Therefore, all terms not shown explicitly in
the p-p energy density [see discussion below Eq. (80)] violate the gauge invariance. On the other hand,
products of complex conjugate p-p densities and p-p
densities may be gauge invariant. This obviously is the case for
the pairing, spin, current, and spin-current p-p densities,
while only specific combinations of kinetic, spin-kinetic, and
tensor-kinetic densities are gauge invariant.
Complete list of all p-h and p-p gauge-invariant
combinations of local densities reads
where 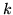 =0,1,2,3, and
=0,1,2,3, and
where 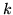 =1,2,3. Note that terms of the p-p energy density
that depend on
=1,2,3. Note that terms of the p-p energy density
that depend on
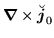 and
and
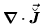 are not gauge invariant.
are not gauge invariant.
Finally, energy density given by Eqs. (78) and (80)
is gauge invariant provided the coupling constants fulfill the
following constraints,
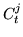 |
 |
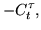 |
(107) |
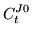 |
 |
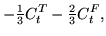 |
(108) |
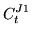 |
 |
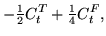 |
(109) |
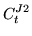 |
 |
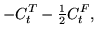 |
(110) |
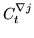 |
 |
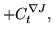 |
(111) |
for 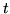 =0,1, and
=0,1, and
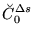 |
 |
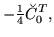 |
(112) |
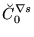 |
 |
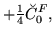 |
(113) |
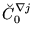 |
 |
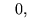 |
(114) |
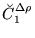 |
 |
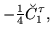 |
(115) |
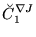 |
 |
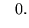 |
(116) |



Next: Skyrme interaction energy functional
Up: The Energy Density Functional
Previous: The Energy Density Functional
Jacek Dobaczewski
2004-01-03