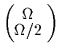 ,
and this puts the practical limit at
,
and this puts the practical limit at
In this section, we investigate
the deformed-shell-plus-pairing Hamiltonian
that contains the single-particle term (17)
(for ![]() twofold degenerate single-particle states
available for the pair scattering)
and seniority-pairing interaction (14).
In this case,
the analytic solution does not exist, but the exact
eigenstates can be found numerically using, for example,
the Richardson method [29]
or by performing
a direct diagonalization. The latter approach
cannot be applied when the number of single-particle
levels is large, because the dimension
of the Hilbert space grows as
twofold degenerate single-particle states
available for the pair scattering)
and seniority-pairing interaction (14).
In this case,
the analytic solution does not exist, but the exact
eigenstates can be found numerically using, for example,
the Richardson method [29]
or by performing
a direct diagonalization. The latter approach
cannot be applied when the number of single-particle
levels is large, because the dimension
of the Hilbert space grows as
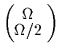 ,
and this puts the practical limit at
,
and this puts the practical limit at
![]() .
imaginary-time method
.
imaginary-time method
A particular variant of this model is when the single-particle
spectrum is uniformly spaced (finite-number equidistant-level model),
i.e.,
ek=kd (k=1,...,![]() ). In this work, we are mainly interested
in the ability of the energy-spacing filter (7)
to extract the single-particle spectrum from the total
binding energies. Therefore, below, we also study the case of
a nearly-equidistant spectrum, in which
ek=kd except for the seventh level
shifted up in energy by d/4 (i.e,
e7=7.25 d).
The value of the single-particle spacing d constitutes a convenient
energy scale, and below, the results will be expressed as ratios
of all energies and parameters with respect to d.
). In this work, we are mainly interested
in the ability of the energy-spacing filter (7)
to extract the single-particle spectrum from the total
binding energies. Therefore, below, we also study the case of
a nearly-equidistant spectrum, in which
ek=kd except for the seventh level
shifted up in energy by d/4 (i.e,
e7=7.25 d).
The value of the single-particle spacing d constitutes a convenient
energy scale, and below, the results will be expressed as ratios
of all energies and parameters with respect to d.
Figures 4
and 5 show the results of the exact calculations for
the nearly-equidistant spectrum of ![]() =16 levels.
The behavior of the three-mass filter (1)
is illustrated in Fig. 4,
where values of
=16 levels.
The behavior of the three-mass filter (1)
is illustrated in Fig. 4,
where values of
![]() are compared to
are compared to
For G/d=0.1 (weak pairing),
values of
![]() nicely follow the low values
of
nicely follow the low values
of ![]() ,
while those of
,
while those of
![]() are clearly
influenced by the single-particle spectrum and do not at all reflect
the smallness of the pairing correlations.
In particular, the fluctuation
around N=14 (n=7) clearly shows up
in
are clearly
influenced by the single-particle spectrum and do not at all reflect
the smallness of the pairing correlations.
In particular, the fluctuation
around N=14 (n=7) clearly shows up
in
![]() and is absent in
and is absent in
![]() .
.
In the case of intermediate
pairing (G/d=0.3),
![]() behaves rather smoothly, while
behaves rather smoothly, while
![]() zigzags in the region of irregularity in the
spectrum. No direct correspondence between the values of
zigzags in the region of irregularity in the
spectrum. No direct correspondence between the values of
![]() and
and
![]() can be found here. However, with increasing values of G, i.e., when the
static pairing sets in,
can be found here. However, with increasing values of G, i.e., when the
static pairing sets in,
![]() closely approaches
closely approaches ![]() .
This is
nicely illustrated for G/d=0.5. Only in the case of relatively strong
pairing correlations (but still far from the strong pairing limit
discussed in Sec. 3.1.2) is the fluctuation in
.
This is
nicely illustrated for G/d=0.5. Only in the case of relatively strong
pairing correlations (but still far from the strong pairing limit
discussed in Sec. 3.1.2) is the fluctuation in
![]() barely
visible.
barely
visible.
In the case of weak pairing correlations, the corresponding
energy-spacing filters
(7),
shown in Fig. 5, very well
reflect the structure of
![]() .
With an increasing pairing
strength, the pairing Hamiltonian gives rise to a diffused Fermi surface (i.e.,
it smears out the single-particle occupations). Consequently,
the information about the details of the single-particle distribution is then
expected to be washed out. This is clearly seen in Fig. 5,
where
the nearly-equidistant single-particle spacings
are marked by dots.
.
With an increasing pairing
strength, the pairing Hamiltonian gives rise to a diffused Fermi surface (i.e.,
it smears out the single-particle occupations). Consequently,
the information about the details of the single-particle distribution is then
expected to be washed out. This is clearly seen in Fig. 5,
where
the nearly-equidistant single-particle spacings
are marked by dots.
However, it is seen that even in the case of relatively
strong pairing correlations, (G/d=0.4), the symmetric energy-spacing
indicator ![]() gives a qualitative description of the spectrum. Even at G/d=0.5, the
zigzag in
gives a qualitative description of the spectrum. Even at G/d=0.5, the
zigzag in ![]() appears in the right place. As far as
the asymmetric filters
appears in the right place. As far as
the asymmetric filters
![]() are concerned, their behavior
is more strongly influenced by G, and the resulting particle
number dependence
may make them less useful measures of the spectral properties.
are concerned, their behavior
is more strongly influenced by G, and the resulting particle
number dependence
may make them less useful measures of the spectral properties.
In order to assess the quality of the quasi-particle (BCS) approximation for
the binding-energy indicators, in the same model we have
also carried out the BCS calculations.
As seen in Fig. 6, it is only at large values of G that
the
![]() filters (1) which are applied to the BCS energies
approach the exact
results. Especially at intermediate
values of pairing strength, where the static pairing vanishes in
odd-N nuclei,
BCS becomes a rather poor approximation. However, it is clear that
values of
filters (1) which are applied to the BCS energies
approach the exact
results. Especially at intermediate
values of pairing strength, where the static pairing vanishes in
odd-N nuclei,
BCS becomes a rather poor approximation. However, it is clear that
values of
![]() are affected by the single-particle spectrum,
while those of
are affected by the single-particle spectrum,
while those of
![]() are rather insensitive to it.
are rather insensitive to it.
The agreement is significantly better for
the energy-spacing filter ![]() (Fig. 7). Again,
as discussed
above, at large values of pairing strength,
(Fig. 7). Again,
as discussed
above, at large values of pairing strength, ![]() is only a
qualitative measure
of the single-particle splitting.
is only a
qualitative measure
of the single-particle splitting.