| = | ![$\displaystyle {1\over 2} G +
{G^2\over 4d} \left[
S(n)+S(\Omega -n-1)
\right],$](img159.gif) |
(57) | |
| = | ![$\displaystyle {d+G\over 2} +
{G^2\over 4d} \left[
S(n)+S(\Omega -n)
\right],$](img161.gif) |
(58) |
Following Sec. 3.1, one can derive
analytic expressions for the binding energy filters which should
be valid in the limiting cases of weak and strong pairing.
Particularly simple are the weak-pairing expressions. Namely,
Eqs. (21) yield:
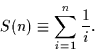 |
(59) |
In the strong-pairing limit of the equidistant-level model,
the zero-order expressions for
![]() and
and ![]() are given by Eqs. (40)
and (41). The corresponding higher-order corrections can be
easily derived using Eqs. (27)-(36)
after noting that
are given by Eqs. (40)
and (41). The corresponding higher-order corrections can be
easily derived using Eqs. (27)-(36)
after noting that
| (63) |
Figure 8
shows the accuracy of the second-order expressions for the binding energies
in the equidistant-level model with ![]() =16
in the weak-pairing (left) and strong-pairing (right) limits.
It is seen that, for large numbers of particles,
the low-
=16
in the weak-pairing (left) and strong-pairing (right) limits.
It is seen that, for large numbers of particles,
the low-![]() expansion is fairly accurate even for
expansion is fairly accurate even for ![]()
![]() 0.4.
Also the
0.4.
Also the ![]() expansion seems to work very well even for large
values of d/G.
different vertical
expansion seems to work very well even for large
values of d/G.
different vertical