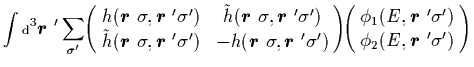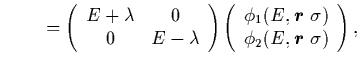Pairing in weakly bound systems

A variational mean-field approach to pairing correlations results in the HFB equations [32]. In weakly bound systems, these equations should be solved in coordinate space in order to properly take into account the closeness of the particle continuum [6,12]. In the most general non-local coordinate representation, the HFB equations have the form of the following matrix integral eigenequation:

 

$$\int\mbox{\scriptsize {d}}^3\mbox{{\boldmath {$r$ }}}' \sum_{\sig... ...'\sigma') \\ \phi_2 (E,\mbox{{\boldmath {$r$ }}}'\sigma') \end{array}\!\right)$$

$$~~~~~~ = \left(\begin{array}{cc} E+\lambda & 0 \\ 0 & E-\lambda ... ...$ }}}\sigma) \\ \phi_2 (E,\mbox{{\boldmath {$r$ }}}\sigma) \end{array}\right),$$ (39)

where E is the quasiparticle energy, $\lambda$ is the Fermi energy, and $h(\mbox{{\boldmath {$r$ }}}\sigma,\mbox{{\boldmath {$r$ }}}'\sigma')$ and $\tilde{h}(\mbox{{\boldmath {$r$ }}}\sigma,\mbox{{\boldmath {$r$ }}}'\sigma')$ are the mean-field particle-hole (p-h) and particle-particle (p-p) Hamiltonians, respectively. Contrary to the HF equations, which define one-component (single-particle) wave functions [the eigenstates of $h(\mbox{{\boldmath {$r$ }}}\sigma,\mbox{{\boldmath {$r$ }}}'\sigma')$], the HFB method gives two-component (quasiparticle) wave functions (the upper and lower components are denoted by $\phi_1(E,\mbox{{\boldmath {$r$ }}}\sigma)$ and $\phi_2(E,\mbox{{\boldmath {$r$ }}}\sigma)$, respectively).

In the following, we solve the HFB equations (39) by fixing the p-h Hamiltonian to be equal to the sum of the kinetic energy (with constant nucleon mass) and PTG' potential (9). In this way, we study self-consistency only in the pairing channel, while the single-particle properties are kept unchanged, and under control. For example, the single-particle energies and resonances do not change during the HFB iteration, and are not affected by the pairing properties, which would have not been the case had we allowed the usual HFB coupling of the p-h and p-p channels. Moreover, within such an approach we only need to solve the HFB equations for neutrons, i.e., for the particles which exhibit the weak binding under study here. Note that for the physical centrifugal barrier included in all the L>0 partial waves, the energies of single-particle bound states and resonances are not given by analytical expressions (29) and (32). However, the barrier does not appear in the s_1/2 channel, and these energies are still given analytically.

Two parameters of the PTG potential have been fixed at values used in the previous Sections, namely, $\Lambda$=7 and s=0.04059, while the depths parameters $\nu_{Lj}$ (Tables 2 and 3) have been chosen in such a way [48] as to simulate a hypothetical single-particle neutron spectrum in drip-line nuclei with N$\simeq$82. For the scope of the present study, details of this spectrum are insignificant; we only aim at realizing the physical situation where the PTG' 3s_1/2 or 2d_3/2 states are near the threshold (close to zero binding energy) and at the same time the Fermi energy is negative and small.

Contrary to the p-h channel, the full self-consistency is required in the p-p channel, with the p-p Hamiltonian given by the local pairing potential [6,12]:

$$\tilde{h}(\mbox{{\boldmath {$r$ }}}\sigma,\mbox{{\boldmath {$... ... {$r$ }}}-\mbox{{\boldmath {$r$ }}}')\delta_{\sigma,\sigma'} ,$$ (40)

where

$$\tilde{U}(\mbox{{\boldmath {$r$ }}})={1\over2}V_0 \tilde{\rho}(\mbox{{\boldmath {$r$ }}}) ,$$ (41)

and

$$\tilde{\rho} = - \sum_{0<E_n<E_{\mbox{\scriptsize {max}}}} \... ...r$ }}}\sigma) \phi^*_1(E_n,\mbox{{\boldmath {$r$ }}}\sigma) .$$ (42)

Potential (41) corresponds to the pairing force given by the zero-range interaction,

$$V(\mbox{{\boldmath {$r$ }}}_1-\mbox{{\boldmath {$r$ }}}_2)=V... ...elta(\mbox{{\boldmath {$r$ }}}_1-\mbox{{\boldmath {$r$ }}}_2).$$ (43)

Strength parameter V₀ has been arbitrarily fixed at V₀=-175MeVfm³. The pairing phase space, given by the cut-off parameter $E_{\mbox{\scriptsize {max}}}$, has been fixed according to the prescription formulated in Ref. [6]. In Eq. (42) we used the fact that in order to discretize the continuum HFB states, the HFB equation is solved in a suitable spatial box. The HFB results presented below have been obtained with the same box size of $R_{\mbox{\scriptsize {box}}}$=30fm as those discussed in Sec. 4.3.

As seen from Eqs. (39)-(41), the intensity of the pairing coupling [i.e., the off-diagonal term in Eq. (39)] is given by the integral of the wave functions with the pairing density $\tilde{\rho}(\mbox{{\boldmath {$r$ }}})$. This integral can be approximated in the following way:

$$\int\mbox{\scriptsize {d}}^3\mbox{{\boldmath {$r$ }}}\sum_{\... ...gma) \simeq \tilde{\rho}_0 \left(N_n L[\phi^*_1]\right)^{1/2},$$ (44)

where $L[\phi^*_1]$ is the localization of the upper HFB wave function, defined as in Eq. (38), and N_n is the norm of the lower HFB wave function:

$$N_n = \int\mbox{\scriptsize {d}}^3\mbox{{\boldmath {$r$ }}}\... ...a} \vert\phi_2(E_n,\mbox{{\boldmath {$r$ }}} \sigma )\vert^2.$$ (45)

Equation (44) gives only a very crude approximation, which aims only at showing the main trends. It is based on two assumptions: (i) that the pairing potential is constant within the radius $R_{\mbox{\scriptsize {Loc}}}$ of the sphere for which the localization is defined, and zero otherwise. Zero-range pairing force (43) leads to the volume-type pairing correlations [12], for which the pairing densities are spread throughout the nucleus, and can be crudely approximated by a constant value $\tilde{\rho}_0$. Another assumption is: (ii) that the lower and upper HFB wave functions are proportional to one another within the radius of $R_{\mbox{\scriptsize {Loc}}}$. We know that this assumption holds only in the BCS approximation, while in the HFB approach the lower and upper components are different, including different nodal structure [12]. For all energies E_n, the lower components are localized inside the nucleus, and their norms N_n give contributions to the particle number (see examples of numerical values presented in Ref. [12] and in the following subsections). On the other hand, the continuum upper HFB wave functions behave asymptotically as plane waves, however, their pairing coupling is dictated by their localizations. We are not going to use Eq. (44) in any quantitative way; we only use it as a motivation to look at localizations of the upper HFB components as measures of how strongly given continuum states contribute to pairing correlations.