The PTG potential depends on four parameters: ![]() which
determines its shape and diffuseness,
which
determines its shape and diffuseness, ![]() which defines its depth,
s (in fm-1) which is a scaling factor that can be adjusted to
obtain a given mean radius of the potential, and a, which allows to
account for an effective mass of the particle. In the present study,
the effective mass is not discussed, and therefore we take a=0, for
which the radial PTG potential is defined as:
which defines its depth,
s (in fm-1) which is a scaling factor that can be adjusted to
obtain a given mean radius of the potential, and a, which allows to
account for an effective mass of the particle. In the present study,
the effective mass is not discussed, and therefore we take a=0, for
which the radial PTG potential is defined as:
Parameter ![]() can take any positive value. (Potentials with
can take any positive value. (Potentials with
![]() <1, for which in Eq. (5) function
<1, for which in Eq. (5) function ![]() changes into
changes into
![]() ,
will not be considered in the present
study.) In principle, parameters
,
will not be considered in the present
study.) In principle, parameters ![]() ,
,
![]() ,
and s can take
different values for every value of L and j. However, below we
use (Lj)-independent values of shape parameter
,
and s can take
different values for every value of L and j. However, below we
use (Lj)-independent values of shape parameter ![]() and
scaling factor s. On the other hand, as indicated in
Eq. (2), values of depth parameter
and
scaling factor s. On the other hand, as indicated in
Eq. (2), values of depth parameter ![]() are independently
chosen for each L and j, so as to obtain 'reasonable'
single-particle spectra, and in particular, to simulate the
spin-orbit splitting of single-particle levels which is absent in the
PTG potential.
are independently
chosen for each L and j, so as to obtain 'reasonable'
single-particle spectra, and in particular, to simulate the
spin-orbit splitting of single-particle levels which is absent in the
PTG potential.
Problem of the nonstandard centrifugal barrier (3) deserves
a few words of discussion.
At the origin (
![]() ), y decreases as
), y decreases as ![]() ,
,
![]() ,
and therefore,
,
and therefore,
| (6) |
| (7) |
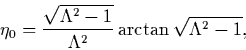 |
(8) |
For small values of ![]() ,
the PTG potential is wide and diffuse.
In Fig. 1 (lower panel) we present the PTG potentials for
L=0 and
,
the PTG potential is wide and diffuse.
In Fig. 1 (lower panel) we present the PTG potentials for
L=0 and
![]() =1, 3, and 7, with parameters s and
=1, 3, and 7, with parameters s and ![]() (Table
8) chosen in such a way as to keep the depth and radius of
the potential fixed. For
(Table
8) chosen in such a way as to keep the depth and radius of
the potential fixed. For ![]() and
and ![]() =0 (see Fig. 1),
one obtains the Pöschl-Teller
potential [45,46] which has been widely studied, e.g., in the
molecular physics. For larger values of
=0 (see Fig. 1),
one obtains the Pöschl-Teller
potential [45,46] which has been widely studied, e.g., in the
molecular physics. For larger values of
![]() ,
the PTG potential gets steeper and resembles the
Woods-Saxon potential. For relatively large values of
,
the PTG potential gets steeper and resembles the
Woods-Saxon potential. For relatively large values of ![]() and
relatively small values of the depth parameter, one may find a small
barrier at the edge of the potential well. Finally, for still larger
and
relatively small values of the depth parameter, one may find a small
barrier at the edge of the potential well. Finally, for still larger
![]() ,
the PTG potential resembles the finite-depth square well
potential. The PTG potentials presented in Fig. 1 for
,
the PTG potential resembles the finite-depth square well
potential. The PTG potentials presented in Fig. 1 for
![]() =3 and 7 correspond to the profiles which are interesting
from the point of view of simulating the nuclear mean field within a
physical range of the diffuseness.
=3 and 7 correspond to the profiles which are interesting
from the point of view of simulating the nuclear mean field within a
physical range of the diffuseness.
In the middle panel of Fig. 1 we present the L=4 radial PTG potentials, again for ![]() =1, 3, and 7, and
parameters s and
=1, 3, and 7, and
parameters s and ![]() given in Table 8.
Similarly, the top panel (with the corresponding parameters s and
given in Table 8.
Similarly, the top panel (with the corresponding parameters s and
![]() )
shows the L=4 potentials for the PTG
centrifugal barrier s2c(R) replaced by the physical centrifugal
barrier. One can see that up to a little beyond the minimum, the PTG
potential reproduces fairly well the potential with the physical
barrier. However, at larger distances, the PTG centrifugal term
disappears too quickly.
)
shows the L=4 potentials for the PTG
centrifugal barrier s2c(R) replaced by the physical centrifugal
barrier. One can see that up to a little beyond the minimum, the PTG
potential reproduces fairly well the potential with the physical
barrier. However, at larger distances, the PTG centrifugal term
disappears too quickly.
Nature of the energy eigenstates inside the potential well, as well
as the nature of scattering solutions, depend strongly on the shape
parameter ![]() .
The smaller is the value of
.
The smaller is the value of ![]() ,
the
broader are the single-particle resonances. Below the critical value of
,
the
broader are the single-particle resonances. Below the critical value of
![]() ,
the resonances entirely disappear,
i.e., there are no single-particle resonant states in any partial
wave anymore.
,
the resonances entirely disappear,
i.e., there are no single-particle resonant states in any partial
wave anymore.