


Next: Enhancement of Schiff Moments
Up: Time-reversal violating Schiff moment
Previous: Time-reversal violating Schiff moment
Introduction
Experiments with K and B mesons indicate that time-reversal invariance (T) is
violated through phases in the Cabibbo-Kobayashi-Maskawa matrix that affect
weak interactions [Naboulsi()]. The suspicion that extra-Standard-Model
physics, e.g. supersymmetry, also violates T has motivated a different kind
of experiment: measuring the electric dipole moments (EDMs) of the neutron
and of atoms. Because any such dipole moment must be proportional to the
expectation value of the T-odd spin operator, it can only exist when T (and
parity) is violated [Sachs(1987),Khriplovich and Lamoreaux(1997)]. So far the experiments have
seen no dipole moments, but they continue to improve and even null results are
useful, since they seriously constrain new physics. Whatever the experimental
situation in the future, therefore, it is important to determine theoretically
what the presence or absence of EDMs at a given level implies about
T-violating interactions at elementary-particle scales. Our focus here is
atoms, which for some sources of T violation currently provide limits as good
or better than the neutron [Romalis et al.(2001)Romalis, Griffith,
Jacobs, and Fortson].
One way an atom can develop an EDM is through T and P violation in its
nucleus. Let us assume that given a fundamental source of the broken symmetry
one can use effective-field theory and QCD to calculate the strength of the
resulting T-violating nucleon-pion interaction. One then needs to connect the
strength of that interaction to the resulting nuclear ``Schiff moment'',
which, because the nuclear EDM is screened [Schiff(1963)], is the quantity
responsible for inducing an EDM in electrons orbiting the nucleus. The Schiff
moment is defined classically as a kind of radially weighted dipole moment:
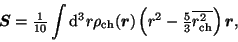 |
(1) |
where 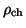 is the nuclear charge density and
is the nuclear charge density and
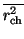 is the mean-square charge radius. Recent papers
[Spevak et al.(1997)Spevak, Auerbach,
and
Flambaum,Auerbach et al.(1996)Auerbach,
Flambaum,
and Spevak] have argued that because of their asymmetric
shapes, octupole-deformed nuclei in the light-actinide region should have
collective Schiff moments that are 100 to 1000 times larger than the Schiff
moment in
is the mean-square charge radius. Recent papers
[Spevak et al.(1997)Spevak, Auerbach,
and
Flambaum,Auerbach et al.(1996)Auerbach,
Flambaum,
and Spevak] have argued that because of their asymmetric
shapes, octupole-deformed nuclei in the light-actinide region should have
collective Schiff moments that are 100 to 1000 times larger than the Schiff
moment in  Hg, the system with the best experimental limit on its
atomic EDM [Romalis et al.(2001)Romalis, Griffith,
Jacobs, and Fortson]. Ref. [Engel et al.(1999)Engel, Friar, and
Hayes] suggested that certain
many-body effects may make the enhancement a bit less than that. The degree
of enhancement is important because several experiments in the light
actinides
are contemplated, planned, or underway [Chupp(),Holt()]. They may see
nonzero EDMs, and even if they don't we will need to be able to compare their
limits on fundamental sources of T violation to those of experiments in other
isotopes.
Hg, the system with the best experimental limit on its
atomic EDM [Romalis et al.(2001)Romalis, Griffith,
Jacobs, and Fortson]. Ref. [Engel et al.(1999)Engel, Friar, and
Hayes] suggested that certain
many-body effects may make the enhancement a bit less than that. The degree
of enhancement is important because several experiments in the light
actinides
are contemplated, planned, or underway [Chupp(),Holt()]. They may see
nonzero EDMs, and even if they don't we will need to be able to compare their
limits on fundamental sources of T violation to those of experiments in other
isotopes.
Perhaps the most attractive octupole-deformed nucleus for an experiment is
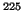 Ra. Though radioactive, it has a ground-state angular momentum
Ra. Though radioactive, it has a ground-state angular momentum
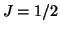 , which minimizes the effect of stray quadrupole electric fields in an
experiment to measure a dipole moment
, which minimizes the effect of stray quadrupole electric fields in an
experiment to measure a dipole moment![[*]](../footnote.png) . In addition, the associated atom has close-lying
electronic levels of opposite parity and is relatively easy to trap and
manipulate. As a result, at least one group is at work on a measurement in
. In addition, the associated atom has close-lying
electronic levels of opposite parity and is relatively easy to trap and
manipulate. As a result, at least one group is at work on a measurement in
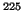 Ra [Holt()]. Here we calculate its Schiff moment, attempting to
incorporate the effects discussed in Ref. [Engel et al.(1999)Engel, Friar, and
Hayes] through a
symmetry-unrestricted mean-field calculation. We begin in the next section
by
describing the physics of the Schiff moment in octupole-deformed nuclei,
briefly reviewing prior work in the process. In Section III we test
our
mean-field approach by calculating properties of even Ra isotopes. In
Section
IV we discuss issues peculiar to mean-field calculations in odd nuclei
and then present our results for the Schiff moment of
Ra [Holt()]. Here we calculate its Schiff moment, attempting to
incorporate the effects discussed in Ref. [Engel et al.(1999)Engel, Friar, and
Hayes] through a
symmetry-unrestricted mean-field calculation. We begin in the next section
by
describing the physics of the Schiff moment in octupole-deformed nuclei,
briefly reviewing prior work in the process. In Section III we test
our
mean-field approach by calculating properties of even Ra isotopes. In
Section
IV we discuss issues peculiar to mean-field calculations in odd nuclei
and then present our results for the Schiff moment of 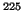 Ra, focusing
particularly on the degree of enhancement. Section V is
a brief conclusion.
Ra, focusing
particularly on the degree of enhancement. Section V is
a brief conclusion.



Next: Enhancement of Schiff Moments
Up: Time-reversal violating Schiff moment
Previous: Time-reversal violating Schiff moment
Jacek Dobaczewski
2003-04-24
![]() Ra. Though radioactive, it has a ground-state angular momentum
Ra. Though radioactive, it has a ground-state angular momentum
![]() , which minimizes the effect of stray quadrupole electric fields in an
experiment to measure a dipole moment
, which minimizes the effect of stray quadrupole electric fields in an
experiment to measure a dipole moment![[*]](../footnote.png) . In addition, the associated atom has close-lying
electronic levels of opposite parity and is relatively easy to trap and
manipulate. As a result, at least one group is at work on a measurement in
. In addition, the associated atom has close-lying
electronic levels of opposite parity and is relatively easy to trap and
manipulate. As a result, at least one group is at work on a measurement in
![]() Ra [Holt()]. Here we calculate its Schiff moment, attempting to
incorporate the effects discussed in Ref. [Engel et al.(1999)Engel, Friar, and
Hayes] through a
symmetry-unrestricted mean-field calculation. We begin in the next section
by
describing the physics of the Schiff moment in octupole-deformed nuclei,
briefly reviewing prior work in the process. In Section III we test
our
mean-field approach by calculating properties of even Ra isotopes. In
Section
IV we discuss issues peculiar to mean-field calculations in odd nuclei
and then present our results for the Schiff moment of
Ra [Holt()]. Here we calculate its Schiff moment, attempting to
incorporate the effects discussed in Ref. [Engel et al.(1999)Engel, Friar, and
Hayes] through a
symmetry-unrestricted mean-field calculation. We begin in the next section
by
describing the physics of the Schiff moment in octupole-deformed nuclei,
briefly reviewing prior work in the process. In Section III we test
our
mean-field approach by calculating properties of even Ra isotopes. In
Section
IV we discuss issues peculiar to mean-field calculations in odd nuclei
and then present our results for the Schiff moment of ![]() Ra, focusing
particularly on the degree of enhancement. Section V is
a brief conclusion.
Ra, focusing
particularly on the degree of enhancement. Section V is
a brief conclusion.