


Next: Mean-field calculations for other
Up: Time-reversal violating Schiff moment
Previous: Introduction
Enhancement of Schiff Moments in Octupole-Deformed Nuclei
- Previous Work
In analogy with dipole moments in atoms, static Schiff moments in nuclei can
exist only if T is broken. Because T-violating forces are much weaker than
the
strong interaction, the Schiff moment can be accurately evaluated through
first-order perturbation theory as
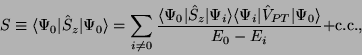 |
(2) |
where
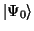 is the member of the ground-state multiplet with
is the member of the ground-state multiplet with
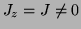 , the sum is over excited states, and
, the sum is over excited states, and 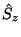 is the operator
is the operator
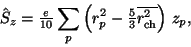 |
(3) |
with the sum here over protons. The operator 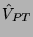 is the T- (and
parity-) violating nucleon-nucleon interaction mediated by the pion
[Haxton and Henley(1983),Herczeg(1988a)] (shown to be more important than other mesons in
Ref. [Towner and Hayes(1994)]):
is the T- (and
parity-) violating nucleon-nucleon interaction mediated by the pion
[Haxton and Henley(1983),Herczeg(1988a)] (shown to be more important than other mesons in
Ref. [Towner and Hayes(1994)]):
![\begin{widetext}
\begin{eqnarray}
\hat{V}_{PT}(\bm{r}_1-\bm{r}_2)
& = - {\disp...
...ac{1}{m_{\pi}\vert\bm{r}_1-\bm{r}_2\vert}
\right]
,
\end{eqnarray}\end{widetext}](img20.png)
where arrows denote isovector operators, 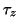 is +1 for neutrons,
is +1 for neutrons,
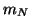 is the nucleon mass, and we
are using
the convention
is the nucleon mass, and we
are using
the convention 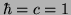 . The
. The 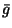 's are the unknown
isoscalar, isovector, and isotensor T-violating pion-nucleon
couplings, and
's are the unknown
isoscalar, isovector, and isotensor T-violating pion-nucleon
couplings, and 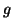 is the usual strong
is the usual strong 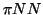 coupling.
coupling.
In a nucleus such as 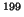 Hg, with no intrinsic octupole deformation, many
intermediate states contribute to the sum in Eq. (2). By
contrast, the asymmetric shape of
Hg, with no intrinsic octupole deformation, many
intermediate states contribute to the sum in Eq. (2). By
contrast, the asymmetric shape of 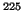 Ra implies the existence of a very
low-energy
Ra implies the existence of a very
low-energy 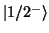 state, in this case 55 keV above the ground state
state, in this case 55 keV above the ground state
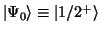 , that dominates the sum because of the
corresponding small denominator. To very good approximation,
then,
, that dominates the sum because of the
corresponding small denominator. To very good approximation,
then,
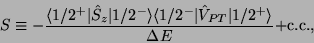 |
(4) |
where 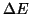 = 55 keV. The small denominator is part of the reason for
the
enhancement of the Schiff moment. The other part is the matrix element of
the
Schiff operator in Eq. (5). In the limit that the deformation
is
rigid, the
ground state and first excited state in octupole-deformed nuclei are
partners
in a parity doublet, i.e., projections onto good parity and angular
momentum of the same ``intrinsic state" that represents the wave function of
the nucleus in its own body-fixed frame. The matrix elements in Eq.
(5) are then proportional (again, in the limit of rigid
deformation) to intrinsic-state expectation values, so that [Spevak et al.(1997)Spevak, Auerbach,
and
Flambaum]
= 55 keV. The small denominator is part of the reason for
the
enhancement of the Schiff moment. The other part is the matrix element of
the
Schiff operator in Eq. (5). In the limit that the deformation
is
rigid, the
ground state and first excited state in octupole-deformed nuclei are
partners
in a parity doublet, i.e., projections onto good parity and angular
momentum of the same ``intrinsic state" that represents the wave function of
the nucleus in its own body-fixed frame. The matrix elements in Eq.
(5) are then proportional (again, in the limit of rigid
deformation) to intrinsic-state expectation values, so that [Spevak et al.(1997)Spevak, Auerbach,
and
Flambaum]
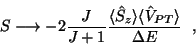 |
(5) |
where 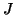 is the ground-state angular momentum, equal to 1/2 for
is the ground-state angular momentum, equal to 1/2 for 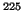 Ra,
and
the brackets indicate expectation values in the intrinsic state. The
intrinsic-state expectation value
Ra,
and
the brackets indicate expectation values in the intrinsic state. The
intrinsic-state expectation value
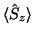 is generated by
the collective quadrupole and octupole deformation of the entire nucleus; it
is much larger than a typical matrix element in a spherical or
symmetrically deformed nucleus. Together with the small energy denominator,
this large matrix element is responsible for the enhancement of
laboratory-frame
Schiff moments in nuclei such as
is generated by
the collective quadrupole and octupole deformation of the entire nucleus; it
is much larger than a typical matrix element in a spherical or
symmetrically deformed nucleus. Together with the small energy denominator,
this large matrix element is responsible for the enhancement of
laboratory-frame
Schiff moments in nuclei such as 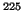 Ra.
Ra.
The amount of the enhancement is not easy to calculate accurately, however.
The
reason is that the matrix element of the two-body spin-dependent operator
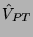 in Eq. (5) depends sensitively on the behavior
of a few valence particles,
which carry most of the spin. In the approximation that particles (or
quasiparticles) move in independent orbits generated by a mean field, the
potential can be written as an effective density-dependent one-body operator
that we will denote
in Eq. (5) depends sensitively on the behavior
of a few valence particles,
which carry most of the spin. In the approximation that particles (or
quasiparticles) move in independent orbits generated by a mean field, the
potential can be written as an effective density-dependent one-body operator
that we will denote 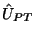 , defined implicitly by
, defined implicitly by
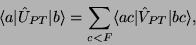 |
(6) |
where 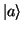 ,
, 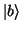 , and
, and 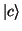 are eigenstates of the mean
field and the matrix elements of
are eigenstates of the mean
field and the matrix elements of 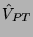 are antisymmetrized. With
the further approximation that the mass of the pion is very large,
are antisymmetrized. With
the further approximation that the mass of the pion is very large,
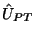 can be written as a local operator, in a form we display in the Section
IV. Evaluating its matrix element is tricky.
can be written as a local operator, in a form we display in the Section
IV. Evaluating its matrix element is tricky.
The authors of Refs. [Spevak et al.(1997)Spevak, Auerbach,
and
Flambaum,Auerbach et al.(1996)Auerbach,
Flambaum,
and Spevak] used a version of the
particle-rotor model [Leander and Sheline(1984)] to represent the odd-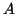 nucleus. In
this
model, all but one of the nucleons are treated as a rigid core, and the last
valence nucleon occupies a deformed single-particle orbit, obtained by
solving
a Schrödinger equation for a Nilsson or deformed Wood-Saxon potential. The
model implies that the core carries no intrinsic spin whatever, that the
neutron and proton densities are proportional, and that the exchange terms on
the right-hand side of Eq. (7) are negligible. Under these
assumptions,
nucleus. In
this
model, all but one of the nucleons are treated as a rigid core, and the last
valence nucleon occupies a deformed single-particle orbit, obtained by
solving
a Schrödinger equation for a Nilsson or deformed Wood-Saxon potential. The
model implies that the core carries no intrinsic spin whatever, that the
neutron and proton densities are proportional, and that the exchange terms on
the right-hand side of Eq. (7) are negligible. Under these
assumptions, 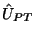 , which now acts only on the single valence
nucleon, reduces to [Sushkov et al.(1984)Sushkov, Flambaum,
and Khriplovich]
, which now acts only on the single valence
nucleon, reduces to [Sushkov et al.(1984)Sushkov, Flambaum,
and Khriplovich]
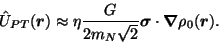 |
(7) |
where 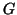 is the Fermi constant,
inserted to follow convention, and
is the Fermi constant,
inserted to follow convention, and 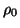 is the total nuclear mass
density. The dimensionless parameter
is the total nuclear mass
density. The dimensionless parameter 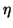 is
then a function of the couplings
is
then a function of the couplings 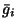 and the isospin of the nucleus.
and the isospin of the nucleus.
Ref. [Engel et al.(1999)Engel, Friar, and
Hayes] confirmed the collectivity of the intrinsic Schiff
moments
obtained in Refs. [Spevak et al.(1997)Spevak, Auerbach,
and
Flambaum,Auerbach et al.(1996)Auerbach,
Flambaum,
and Spevak], but questioned the accuracy of
some of the
assumptions used to evaluate the matrix element of 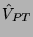 , suggesting
that either core-spin polarization or self-consistency in the
nuclear wave function might reduce laboratory Schiff moments. The zero-range
approximation and the neglect of exchange in
, suggesting
that either core-spin polarization or self-consistency in the
nuclear wave function might reduce laboratory Schiff moments. The zero-range
approximation and the neglect of exchange in 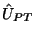 are also open
to question. As a result, it is not clear whether the Schiff moment of
are also open
to question. As a result, it is not clear whether the Schiff moment of
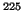 Ra is 1000 times that of
Ra is 1000 times that of 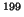 Hg or 100 times, or even less. In
what
follows, we provide a (tentative) answer by moving
beyond the particle-rotor model. Our calculation is not the final word on
Schiff moments in octupole-deformed nuclei -- we only do mean-field
theory, neglecting in particular to project onto states with good parity, and
do not fully account for the pion's nonzero range -- but is a major step
forward.
Hg or 100 times, or even less. In
what
follows, we provide a (tentative) answer by moving
beyond the particle-rotor model. Our calculation is not the final word on
Schiff moments in octupole-deformed nuclei -- we only do mean-field
theory, neglecting in particular to project onto states with good parity, and
do not fully account for the pion's nonzero range -- but is a major step
forward.



Next: Mean-field calculations for other
Up: Time-reversal violating Schiff moment
Previous: Introduction
Jacek Dobaczewski
2003-04-24
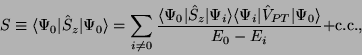
![\begin{widetext}
\begin{eqnarray}
\hat{V}_{PT}(\bm{r}_1-\bm{r}_2)
& = - {\disp...
...ac{1}{m_{\pi}\vert\bm{r}_1-\bm{r}_2\vert}
\right]
,
\end{eqnarray}\end{widetext}](img20.png)
![]() Hg, with no intrinsic octupole deformation, many
intermediate states contribute to the sum in Eq. (2). By
contrast, the asymmetric shape of
Hg, with no intrinsic octupole deformation, many
intermediate states contribute to the sum in Eq. (2). By
contrast, the asymmetric shape of ![]() Ra implies the existence of a very
low-energy
Ra implies the existence of a very
low-energy ![]() state, in this case 55 keV above the ground state
state, in this case 55 keV above the ground state
![]() , that dominates the sum because of the
corresponding small denominator. To very good approximation,
then,
, that dominates the sum because of the
corresponding small denominator. To very good approximation,
then,
![]() in Eq. (5) depends sensitively on the behavior
of a few valence particles,
which carry most of the spin. In the approximation that particles (or
quasiparticles) move in independent orbits generated by a mean field, the
potential can be written as an effective density-dependent one-body operator
that we will denote
in Eq. (5) depends sensitively on the behavior
of a few valence particles,
which carry most of the spin. In the approximation that particles (or
quasiparticles) move in independent orbits generated by a mean field, the
potential can be written as an effective density-dependent one-body operator
that we will denote ![]() , defined implicitly by
, defined implicitly by
![]() nucleus. In
this
model, all but one of the nucleons are treated as a rigid core, and the last
valence nucleon occupies a deformed single-particle orbit, obtained by
solving
a Schrödinger equation for a Nilsson or deformed Wood-Saxon potential. The
model implies that the core carries no intrinsic spin whatever, that the
neutron and proton densities are proportional, and that the exchange terms on
the right-hand side of Eq. (7) are negligible. Under these
assumptions,
nucleus. In
this
model, all but one of the nucleons are treated as a rigid core, and the last
valence nucleon occupies a deformed single-particle orbit, obtained by
solving
a Schrödinger equation for a Nilsson or deformed Wood-Saxon potential. The
model implies that the core carries no intrinsic spin whatever, that the
neutron and proton densities are proportional, and that the exchange terms on
the right-hand side of Eq. (7) are negligible. Under these
assumptions, ![]() , which now acts only on the single valence
nucleon, reduces to [Sushkov et al.(1984)Sushkov, Flambaum,
and Khriplovich]
, which now acts only on the single valence
nucleon, reduces to [Sushkov et al.(1984)Sushkov, Flambaum,
and Khriplovich]
![]() , suggesting
that either core-spin polarization or self-consistency in the
nuclear wave function might reduce laboratory Schiff moments. The zero-range
approximation and the neglect of exchange in
, suggesting
that either core-spin polarization or self-consistency in the
nuclear wave function might reduce laboratory Schiff moments. The zero-range
approximation and the neglect of exchange in ![]() are also open
to question. As a result, it is not clear whether the Schiff moment of
are also open
to question. As a result, it is not clear whether the Schiff moment of
![]() Ra is 1000 times that of
Ra is 1000 times that of ![]() Hg or 100 times, or even less. In
what
follows, we provide a (tentative) answer by moving
beyond the particle-rotor model. Our calculation is not the final word on
Schiff moments in octupole-deformed nuclei -- we only do mean-field
theory, neglecting in particular to project onto states with good parity, and
do not fully account for the pion's nonzero range -- but is a major step
forward.
Hg or 100 times, or even less. In
what
follows, we provide a (tentative) answer by moving
beyond the particle-rotor model. Our calculation is not the final word on
Schiff moments in octupole-deformed nuclei -- we only do mean-field
theory, neglecting in particular to project onto states with good parity, and
do not fully account for the pion's nonzero range -- but is a major step
forward.