

Next: Parity, and signature or
Up: Single-particle bases for conserved
Previous: Time-reversal, and T-signature or
Time-reversal, and signature or simplex
For operators
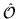 ,
for which both Eq. (11) and (18) hold,
matrix
,
for which both Eq. (11) and (18) hold,
matrix 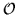 in Eq. (13) can be additionally simplified,
and reads
in Eq. (13) can be additionally simplified,
and reads
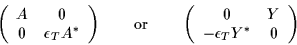 |
(26) |
for
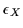 =+1 and
=+1 and
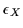 =-1, respectively, with
A hermitian, and Y antisymmetric (
=-1, respectively, with
A hermitian, and Y antisymmetric (
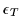 =+1)
or symmetric (
=+1)
or symmetric (
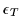 =-1). Of course, this case is
identical to that described in Sec. 3.1.5, because
whenever the time-reversal, and signature or simplex are conserved, the
corresponding T-signature or T-simplex are also conserved,
and
=-1). Of course, this case is
identical to that described in Sec. 3.1.5, because
whenever the time-reversal, and signature or simplex are conserved, the
corresponding T-signature or T-simplex are also conserved,
and
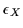 =
=
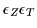 .
Therefore, we may now use two different bases, and obtain two different
forms of the matrix
.
Therefore, we may now use two different bases, and obtain two different
forms of the matrix 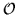 ,
(23) or (26),
which lead either to real, or to block-diagonal matrices.
Note that in order to diagonalize matrix
,
(23) or (26),
which lead either to real, or to block-diagonal matrices.
Note that in order to diagonalize matrix 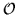 for
for
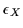 =+1,
one has to diagonalize only its hermitian submatrix A, which has dimension
twice smaller than
=+1,
one has to diagonalize only its hermitian submatrix A, which has dimension
twice smaller than 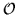 ,
similarly as in Eq. (25).
,
similarly as in Eq. (25).
Jacek Dobaczewski
2000-02-05
![]() ,
for which both Eq. (11) and (18) hold,
matrix
,
for which both Eq. (11) and (18) hold,
matrix ![]() in Eq. (13) can be additionally simplified,
and reads
in Eq. (13) can be additionally simplified,
and reads