

Next: Parity
Up: Single-particle bases for conserved
Previous: T-signature or T-simplex
Signature or simplex
Let us now consider operator
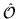 which is even or odd
with respect to one of the six linear D
which is even or odd
with respect to one of the six linear D
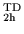 operators,
signatures
operators,
signatures
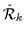 or simplexes
or simplexes
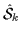 ,
k=x,y,z, which have
squares equal to minus unity, (
,
k=x,y,z, which have
squares equal to minus unity, (
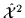 =
=
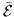 =
=
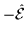 ,
where
,
where
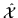 denotes
one of them), i.e.,
denotes
one of them), i.e.,
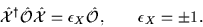 |
(18) |
Since every operator
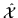 commutes with the time-reversal
commutes with the time-reversal
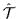 ,
one can always
choose a basis in which Eq. (9) holds,
and
,
one can always
choose a basis in which Eq. (9) holds,
and
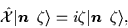 |
(19) |
where again 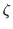 =
=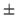 1, so r=
1, so r=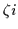 =
=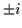 is the signature
(for
is the signature
(for
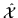 =
=
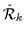 )
or simplex s=
)
or simplex s=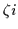 =
=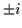 (for
(for
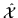 =
=
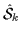 )
quantum number.
Table 4 lists
such bases constructed for the HO states
|nxnynz,sz=
)
quantum number.
Table 4 lists
such bases constructed for the HO states
|nxnynz,sz=
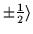 .
A similar construction
is possible for any other single-particle basis. Note that
one can arbitrarily change the phases of states
.
A similar construction
is possible for any other single-particle basis. Note that
one can arbitrarily change the phases of states
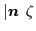 =
=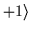 ,
and still fulfill Eqs. (9) and (19); we shall use this
freedom in Secs. 3.1.8 and 3.2.
,
and still fulfill Eqs. (9) and (19); we shall use this
freedom in Secs. 3.1.8 and 3.2.
From Eqs. (18) and (19) one gets:
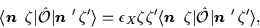 |
(20) |
so the matrix 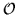 has the form
has the form
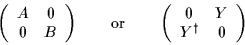 |
(21) |
for
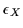 =+1 and
=+1 and
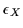 =-1, respectively,
with A and B hermitian, and Y arbitrary complex matrix.
Note that in
order to diagonalize
=-1, respectively,
with A and B hermitian, and Y arbitrary complex matrix.
Note that in
order to diagonalize 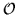 one only needs to
diagonalize: (i) for
one only needs to
diagonalize: (i) for
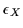 =+1, two hermitian matrices
with complex, in general, submatrices
in twice smaller dimension, which gives real
eigenvalues with no additional restrictions,
or (ii) for
=+1, two hermitian matrices
with complex, in general, submatrices
in twice smaller dimension, which gives real
eigenvalues with no additional restrictions,
or (ii) for
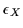 =-1, one hermitian
matrix
=-1, one hermitian
matrix
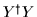 ,
again with complex submatrices in twice smaller dimension,
which gives pairs of real non-zero eigenvalues with opposite signs.
,
again with complex submatrices in twice smaller dimension,
which gives pairs of real non-zero eigenvalues with opposite signs.
Table 4:
Eigenstates
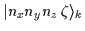 of the signature or
simplex operators,
of the signature or
simplex operators,
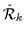 or
or
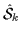 for
k=x, y, or z, [cf. Eqs. (9) and (19)],
determined
for the harmonic oscillator states
|nxnynz,sz=
for
k=x, y, or z, [cf. Eqs. (9) and (19)],
determined
for the harmonic oscillator states
|nxnynz,sz=
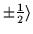 .
Symbols
(Nx,Ny,Nz) refer to
(nx,ny,nz) for
.
Symbols
(Nx,Ny,Nz) refer to
(nx,ny,nz) for
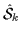 operators, and to (ny+nz,nx+nz,nx+ny) for
operators, and to (ny+nz,nx+nz,nx+ny) for
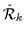 operators.
Phases of eigenstates are fixed so as to fulfill condition
(41).
operators.
Phases of eigenstates are fixed so as to fulfill condition
(41).
| k |
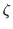 |
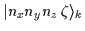 |
| | |
| x |
+1 |
|
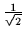 |
(|nxnynz,sz=
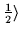 | - |
(-1)Nx |
|nxnynz,sz=
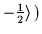 |
| x |
-1 |
|
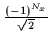 |
(|nxnynz,sz=
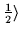 | + |
(-1)Nx |
|nxnynz,sz=
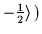 |
| y |
+1 |
|
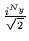 |
(|nxnynz,sz=
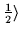 | - |
i(-1)Ny |
|nxnynz,sz=
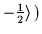 |
| y |
-1 |
|
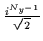 |
(|nxnynz,sz=
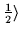 | + |
i(-1)Ny |
|nxnynz,sz=
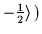 |
| z |
+1 |
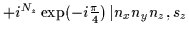 = =
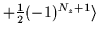 |
| | |
| z |
-1 |
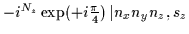 = =
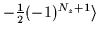 |
| | |
Comparing result (21) with that obtained in
Sec. 3.1.2, one sees that the antilinear symmetries allow for
using real matrices, while linear symmetries give special
block-diagonal forms for complex matrices.


Next: Parity
Up: Single-particle bases for conserved
Previous: T-signature or T-simplex
Jacek Dobaczewski
2000-02-05
![]() which is even or odd
with respect to one of the six linear D
which is even or odd
with respect to one of the six linear D
![]() operators,
signatures
operators,
signatures
![]() or simplexes
or simplexes
![]() ,
k=x,y,z, which have
squares equal to minus unity, (
,
k=x,y,z, which have
squares equal to minus unity, (
![]() =
=
![]() =
=
![]() ,
where
,
where
![]() denotes
one of them), i.e.,
denotes
one of them), i.e.,