

Next: Signature or simplex
Up: Single-particle bases for conserved
Previous: Time-reversal
T-signature or T-simplex
As is well known[17,6], for each of the six antilinear D
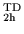 operators, i.e., for T-signature
operators, i.e., for T-signature
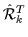 or T-simplex
or T-simplex
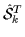 ,
k=x,y,z, which have
squares equal to unity, (
,
k=x,y,z, which have
squares equal to unity, (
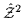 =
=
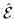 ,
where
,
where
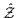 denotes one
of them), one can construct a basis composed of eigenvectors of
denotes one
of them), one can construct a basis composed of eigenvectors of
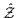 with eigenvalue equal to 1,
with eigenvalue equal to 1,
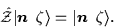 |
(14) |
Moreover, since every
operator
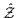 commutes with the time-reversal
commutes with the time-reversal
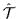 ,
such basis can
always be chosen so as to fulfill condition
(9) at the same time. Table 3 lists
examples of such bases, constructed for the HO states
|nxnynz,sz=
,
such basis can
always be chosen so as to fulfill condition
(9) at the same time. Table 3 lists
examples of such bases, constructed for the HO states
|nxnynz,sz=
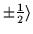 .
A similar construction
is possible for any other single-particle basis, and has the explicit
form shown in Table 3 provided
the space and spin degrees of freedom are separated. Note that
any linear combination of states
.
A similar construction
is possible for any other single-particle basis, and has the explicit
form shown in Table 3 provided
the space and spin degrees of freedom are separated. Note that
any linear combination of states
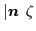 =
=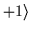 and
and
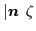 =
=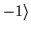 ,
with real coefficients, is
another valid eigenstate of
,
with real coefficients, is
another valid eigenstate of
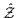 with eigenvalue 1.
with eigenvalue 1.
For operators even or odd with respect to
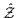 ,
,
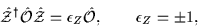 |
(15) |
one then has
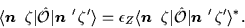 |
(16) |
Hence, in bases fulfilling Eqs. (9) and (14),
matrix 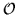 is purely real
(
is purely real
(
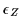 =+1) or purely imaginary (
=+1) or purely imaginary (
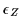 =-1). This gives
matrix
=-1). This gives
matrix 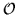 in the form (tilde stands for the transposition)
in the form (tilde stands for the transposition)
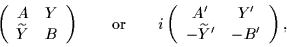 |
(17) |
for
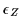 =+1 and
=+1 and
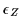 =-1, respectively,
where all submatrices are real, A and B are symmetric, A' and B' are
antisymmetric, and Y and Y' are arbitrary.
Note that in order to diagonalize
=-1, respectively,
where all submatrices are real, A and B are symmetric, A' and B' are
antisymmetric, and Y and Y' are arbitrary.
Note that in order to diagonalize 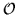 one only needs to diagonalize a real matrix with unrestricted
eigenvalues (for
one only needs to diagonalize a real matrix with unrestricted
eigenvalues (for
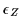 =+1),
or an imaginary matrix with pairs of opposite non-zero
eigenvalues (for
=+1),
or an imaginary matrix with pairs of opposite non-zero
eigenvalues (for
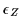 =-1).
=-1).
Table 3:
Examples of eigenstates
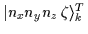 of
the T-signature,
of
the T-signature,
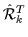 ,
or
T-simplex,
,
or
T-simplex,
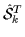 operators,
k=x, y, or z, with eigenvalue 1
[cf. Eqs. (9) and (14)],
determined
for the harmonic oscillator states
|nxnynz,sz=
operators,
k=x, y, or z, with eigenvalue 1
[cf. Eqs. (9) and (14)],
determined
for the harmonic oscillator states
|nxnynz,sz=
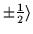 .
Symbols
(Nx,Ny,Nz) refer to
(nx,ny,nz) for
.
Symbols
(Nx,Ny,Nz) refer to
(nx,ny,nz) for
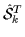 operators, and to (ny+nz,nx+nz,nx+ny) for
operators, and to (ny+nz,nx+nz,nx+ny) for
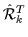 operators.
operators.
| k |
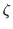 |
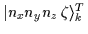 |
| | |
| x |
+1 |
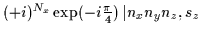 = =
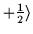 |
| | |
| x |
-1 |
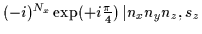 = =
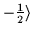 |
| | |
| y |
+1 |
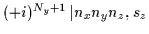 = =
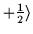 |
| | |
| y |
-1 |
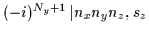 = =
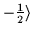 |
| | |
| z |
+1 |
|
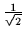 | (
|nxnynz,sz=
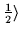 | + |
i(-1)Nz |
|nxnynz,sz=
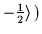 |
| z |
-1 |
|
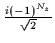 | (
|nxnynz,sz=
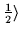 | - |
i(-1)Nz |
|nxnynz,sz=
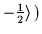 |


Next: Signature or simplex
Up: Single-particle bases for conserved
Previous: Time-reversal
Jacek Dobaczewski
2000-02-05
![]() operators, i.e., for T-signature
operators, i.e., for T-signature
![]() or T-simplex
or T-simplex
![]() ,
k=x,y,z, which have
squares equal to unity, (
,
k=x,y,z, which have
squares equal to unity, (
![]() =
=
![]() ,
where
,
where
![]() denotes one
of them), one can construct a basis composed of eigenvectors of
denotes one
of them), one can construct a basis composed of eigenvectors of
![]() with eigenvalue equal to 1,
with eigenvalue equal to 1,
![]() ,
,