

Next: THO and Gauss integration
Up: Transformed Harmonic Oscillator Basis
Previous: Parametrization of the LST
In the present study, we restrict our HFB analysis to shapes having axial
symmetry. For this purpose, we use HO wave functions in cylindrical coordinates,
z, 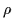 ,
and
,
and 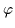 ,
,
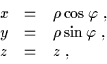 |
(20) |
which allows us to separate the HFB equations into
blocks with good projection 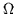 of the angular momentum on the symmetry
axis. [Note that the use of cylindrical coordinates is independent of working
with equal oscillator lengths (13).] Since the use of a cylindrical HO
basis is by now a standard technique (see, e.g., Ref. [16]), we give
here only the information pertaining to constructing the cylindrical THO states.
of the angular momentum on the symmetry
axis. [Note that the use of cylindrical coordinates is independent of working
with equal oscillator lengths (13).] Since the use of a cylindrical HO
basis is by now a standard technique (see, e.g., Ref. [16]), we give
here only the information pertaining to constructing the cylindrical THO states.
The cylindrical HO basis wave functions are given explicitly by
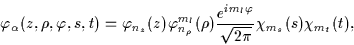 |
(21) |
where the spin s and isospin tdegrees of freedom are shown explicitly, nz and 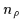 are the number of
nodes along z and
are the number of
nodes along z and 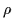 directions, respectively, while ml and msare the components of the orbital angular momentum and the spin along the
symmetry axis. The only conserved quantum numbers in this case are the total
angular momentum projection
directions, respectively, while ml and msare the components of the orbital angular momentum and the spin along the
symmetry axis. The only conserved quantum numbers in this case are the total
angular momentum projection 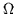 =ml+ms and the parity
=ml+ms and the parity
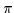 =
(-)nz+ml.
=
(-)nz+ml.
In the axially deformed case, the general LST (1) acts only on the
cylindrical coordinates z and 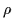 and takes the form
and takes the form
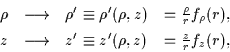 |
(22) |
with the
corresponding Jacobian given by
| D |
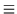 |
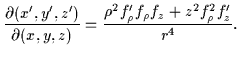 |
(23) |
Finally, the axial THO wave functions are
The assumption of a single oscillator length (see Sect. 2.3) that we make
in our calculations translates in the axial case to
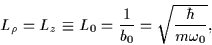 |
(25) |
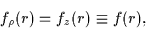 |
(26) |
and the Jacobian (23) reduces to expression
(15).


Next: THO and Gauss integration
Up: Transformed Harmonic Oscillator Basis
Previous: Parametrization of the LST
Jacek Dobaczewski
1999-09-13
![]() ,
and
,
and ![]() ,
,
![]() and takes the form
and takes the form