The HFB state
![]() is a linear combination
of eigenstates
is a linear combination
of eigenstates ![]() of the particle-number operator, i.e.,
of the particle-number operator, i.e.,
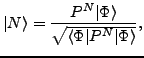 |
(81) |
The HFB+VAPNP variational procedure gives, in principle, the same value of the
projected energy independently of the value of ![]() . This
independence can, however, be subject to numerical instabilities
whenever the amplitude
. This
independence can, however, be subject to numerical instabilities
whenever the amplitude ![]() , corresponding to the projection on
, corresponding to the projection on ![]() particles, is small. Therefore, for practical reasons, one is
interested in keeping the average number of particles
particles, is small. Therefore, for practical reasons, one is
interested in keeping the average number of particles ![]() as
close as possible to
as
close as possible to ![]() , which guarantees that amplitude
, which guarantees that amplitude ![]() is as
large as possible.
is as
large as possible.
In the standard HFB equations (21), the average number of
particles is kept equal to ![]() by adjusting the Lagrange multiplier
by adjusting the Lagrange multiplier
![]() . However, in the HFB+VAPNP approach,
. However, in the HFB+VAPNP approach, ![]() does not
appear in the variational equations (65), because the
variation of the constant term
does not
appear in the variational equations (65), because the
variation of the constant term
![]() equals zero. Therefore, the HFB+VAPNP equations (65) do not
allow for adjusting the average particle number
equals zero. Therefore, the HFB+VAPNP equations (65) do not
allow for adjusting the average particle number ![]() , which, during the
iteration procedure, may become vary different from
, which, during the
iteration procedure, may become vary different from ![]() . Moreover,
such uncontrolled changes of
. Moreover,
such uncontrolled changes of ![]() from one iteration to another
may preclude reaching the stable self-consistent solution.
from one iteration to another
may preclude reaching the stable self-consistent solution.
In order to cope with these problems, one can artificially reintroduce a constant
![]() , analogous to the Fermi energy
, analogous to the Fermi energy ![]() ,
into the HFB+VAPNP equations (65), i.e.,
,
into the HFB+VAPNP equations (65), i.e.,
Had such an ideal situation continued till the end, a nonzero value
of ![]() would have never appeared, and the required solution would
have been found. In practice, this situation never happens, and at
some iteration one finds that
Tr
would have never appeared, and the required solution would
have been found. In practice, this situation never happens, and at
some iteration one finds that
Tr![]() , i.e., the sum of
norms of the second components
, i.e., the sum of
norms of the second components
![]() (68) of
the HFB+VAPNP wave functions, is larger (smaller) than
(68) of
the HFB+VAPNP wave functions, is larger (smaller) than ![]() . In such
a case, in the next iteration one uses a slightly negative (positive)
value of
. In such
a case, in the next iteration one uses a slightly negative (positive)
value of ![]() , which decreases (increases) the norms of
, which decreases (increases) the norms of
![]() , and decreases (increases) the average particle
number in the next iteration. Since
, and decreases (increases) the average particle
number in the next iteration. Since ![]() acts in exactly the same
way as the Fermi energy does within the standard HFB method, the
well-established algorithms of readjusting
acts in exactly the same
way as the Fermi energy does within the standard HFB method, the
well-established algorithms of readjusting ![]() can be used.
Moreover, as soon as the iteration procedure starts to converge, the
non-zero values of
can be used.
Moreover, as soon as the iteration procedure starts to converge, the
non-zero values of ![]() cease to be needed, and thus
cease to be needed, and thus ![]() naturally
converges to zero, as required. In practice, we find that the above
algorithm is very useful, and it provides
the same converged solution with any value of
naturally
converges to zero, as required. In practice, we find that the above
algorithm is very useful, and it provides
the same converged solution with any value of
![]() ,
, ![]() being a small integer.
being a small integer.