


Next: Skyrme HFB+VAPNP procedure: practical
Up: Variation after particle-number projection
Previous: The Lipkin-Nogami method
Following the VAPNP procedure of Sec. 3.1,
one can develop the Skyrme HFB+VAPNP equations
by introducing the gauge-angle-dependent transition
density matrices:
In the above equation, the density matrix
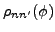 is given by Eq. (36) while
is given by Eq. (36) while
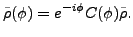 |
(52) |
The associated gauge-angle-dependent local densities
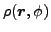 ,
,
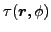 ,
,
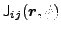 ,
,
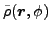 ,
,
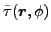 , and
, and
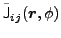 are defined by
Eqs. (18) in terms of the density matrices
(50) and (51). Using the Wick
theorem for matrix elements [2], one can show that the gauge-angle-dependent
transition energy density
are defined by
Eqs. (18) in terms of the density matrices
(50) and (51). Using the Wick
theorem for matrix elements [2], one can show that the gauge-angle-dependent
transition energy density
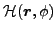 can be obtained from the
intrinsic energy density
can be obtained from the
intrinsic energy density
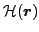 simply by
substituting particle (pairing) local densities with their
gauge-angle-dependent counterparts (e.g.,
simply by
substituting particle (pairing) local densities with their
gauge-angle-dependent counterparts (e.g.,
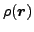
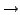
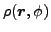 ).
).
In the case of Skyrme functionals, the HFB+VAPNP energy (26)
can be expressed through an integral
![$\displaystyle E^{N}[\rho ,\tilde{\rho}]=\int d\phi ~y(\phi )~E(\phi ),$](img170.png) |
(53) |
where the transition energy reads:
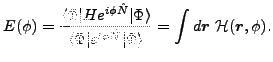 |
(54) |
The projected energy (53)
is a functional
![$ E^{N}[\rho ,\tilde{\rho}]$](img172.png) of the matrix
elements of intrinsic (i.e.,
of the matrix
elements of intrinsic (i.e., 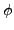 =0) matrices
=0) matrices 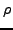 and
and
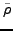 .
.
In order to compute the derivatives of
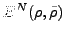 with respect to
with respect to 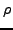 and
and
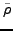 , one should take first
the derivatives of
, one should take first
the derivatives of
![$ E^{N}[\rho ,\tilde{\rho}]$](img172.png) with respect to
with respect to
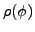 and
and
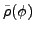 ,
and then the derivatives of
,
and then the derivatives of
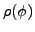 and
and
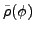 with respect to the intrinsic densities
with respect to the intrinsic densities 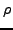 and
and
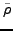 .
For example,
.
For example,
With the use of the identity:
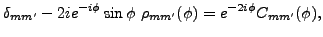 |
(56) |
the partial derivatives in Eq. (55) can easily be
calculated:
where 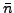 and
and 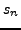 (
(
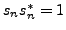 ,
,
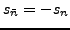 ) are defined using the time-reversal operator
) are defined using the time-reversal operator
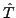 , as
, as
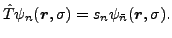 |
(61) |
By inserting Eqs. (57)-(60) in
Eq. (55), the latter reads
where
The derivative of
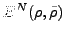 with respect to
with respect to
 can be computed in a similar manner.
The
can be computed in a similar manner.
The  -dependent fields
-dependent fields
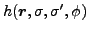 and
and
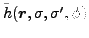 are obtained by substituting the
local particle and pairing densities in the
intrinsic fields
are obtained by substituting the
local particle and pairing densities in the
intrinsic fields
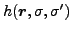 and
and
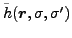 with their
gauge-angle-dependent counterparts.
with their
gauge-angle-dependent counterparts.
The Skyrme HFB+VAPNP equations can finally be written
in the form
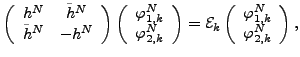 |
(65) |
with particle-hole and particle-particle Hamiltonians
Finally, solutions of the HFB+VAPNP equations
(65) allow for calculating the intrinsic density matrices as,
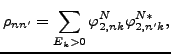 |
|
|
(68) |
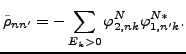 |
|
|
(69) |
Let us re-emphasize that the densities and fields that enter
the Skyrme HFB+VAPNP equations
are immediate generalizations of the analogous quantities that
appear in the standard
Skyrme HFB formalism. Of course, due to
the presence of 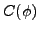 and integrations over the gauge angle,
the Skyrme HFB+VAPNP
calculations are appreciably more involved.
and integrations over the gauge angle,
the Skyrme HFB+VAPNP
calculations are appreciably more involved.



Next: Skyrme HFB+VAPNP procedure: practical
Up: Variation after particle-number projection
Previous: The Lipkin-Nogami method
Jacek Dobaczewski
2006-10-13
![]() with respect to
with respect to ![]() and
and
![]() , one should take first
the derivatives of
, one should take first
the derivatives of
![]() with respect to
with respect to
![]() and
and
![]() ,
and then the derivatives of
,
and then the derivatives of
![]() and
and
![]() with respect to the intrinsic densities
with respect to the intrinsic densities ![]() and
and
![]() .
For example,
.
For example,
![$\displaystyle \frac{\partial E^{N}[\rho ,\tilde{\rho}]}{\partial \rho } =\int d\phi
~y(\phi )~Y(\phi )~E(\phi )$](img198.png)
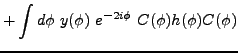
![$\displaystyle -\left[ \int d\phi ~y(\phi )~2ie^{-i\phi }\sin(\phi
)~\tilde{\rho}(\phi )
\tilde{h}(\phi )C(\phi ) + {\rm h.c.}\right],$](img200.png)
![]() and integrations over the gauge angle,
the Skyrme HFB+VAPNP
calculations are appreciably more involved.
and integrations over the gauge angle,
the Skyrme HFB+VAPNP
calculations are appreciably more involved.