




Next: Symetrie i własności Transformaty
Up: Przekształcenie Fouriera
Previous: Przekształcenie Fouriera
Spis tresci
Skorowidz
Szczególna postać wzorów (2.13) i (2.14)
wynika z przyjęcia konwencji wyrażania częstości jako odwrotności czasu:
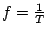 (w hercach). Dowolność pozostaje w umieszczeniu minusa w wykładniku
-- we wzorze na transformatę odwrotną (2.13)
lub we wzorze (2.14). Z kolei przyjęcie częstości kołowej
(w hercach). Dowolność pozostaje w umieszczeniu minusa w wykładniku
-- we wzorze na transformatę odwrotną (2.13)
lub we wzorze (2.14). Z kolei przyjęcie częstości kołowej
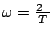 (w radianach) przenosi czynnik
(w radianach) przenosi czynnik 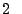 (konkretnie jego odwrotność) z wykładnika przed całkę.
Stąd różnorodność możliwych par wzorów:
(konkretnie jego odwrotność) z wykładnika przed całkę.
Stąd różnorodność możliwych par wzorów:
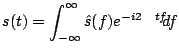 |
|
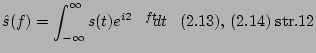 |
|
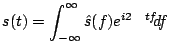 |
|
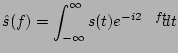 |
(2.16) |
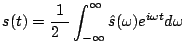 |
|
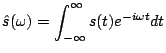 |
(2.17) |
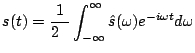 |
|
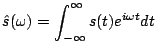 |
(2.18) |
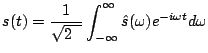 |
|
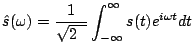 |
(2.19) |
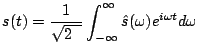 |
|
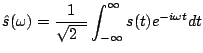 |
(2.20) |
Przyjmiemy wywodzącą się z matematyki konwencję dodatniego wykładnika we wzorze na transformację
(2.14) i ujemnego we wzorze na transformację odwrotną
(2.13); ewentualne stosowanie częstości kołowej można odróżnić po użyciu symbolu
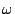 jako argumentu transformaty. W zastosowaniach inżynierskich przeważa konwencja
ujemnego wykładnika we wzorze na transformację (2.16).
jako argumentu transformaty. W zastosowaniach inżynierskich przeważa konwencja
ujemnego wykładnika we wzorze na transformację (2.16).





Next: Symetrie i własności Transformaty
Up: Przekształcenie Fouriera
Previous: Przekształcenie Fouriera
Spis tresci
Skorowidz
Piotr J. Durka
2004-01-05
![]() (w hercach). Dowolność pozostaje w umieszczeniu minusa w wykładniku
-- we wzorze na transformatę odwrotną (2.13)
lub we wzorze (2.14). Z kolei przyjęcie częstości kołowej
(w hercach). Dowolność pozostaje w umieszczeniu minusa w wykładniku
-- we wzorze na transformatę odwrotną (2.13)
lub we wzorze (2.14). Z kolei przyjęcie częstości kołowej
![]() (w radianach) przenosi czynnik
(w radianach) przenosi czynnik ![]() (konkretnie jego odwrotność) z wykładnika przed całkę.
Stąd różnorodność możliwych par wzorów:
(konkretnie jego odwrotność) z wykładnika przed całkę.
Stąd różnorodność możliwych par wzorów: