Korelacja jest miarą podobieństwa lub wzajemnej zależności.
Jeśli mówimy, że występuje korelacja między wydajnością i ceną komputerów,
to mamy na myśli stwierdzenie, że droższe komputery mają zwykle większą
moc obliczeniową -- im mniej przypadków przeciwnych, tym korelacja silniejsza.
Silna korelacja sygnałów ![]() i
i ![]() oznacza, że wzrostowi
oznacza, że wzrostowi ![]() towarzyszy
najczęściej wzrost
towarzyszy
najczęściej wzrost ![]()
![]() .
Jeśli przeważa sytuacja odwrotna
.
Jeśli przeważa sytuacja odwrotna
![]() mówimy o korelacji ujemnej.
mówimy o korelacji ujemnej.
Miarą współzmienności (kowariancji) dwóch sygnałów jest ich iloczyn. Przed obliczeniem tego iloczynu (w ogólnym przypadku mówimy o jego wartości oczekiwanej) od każdego z sygnałów warto odjąć wartość średnią:
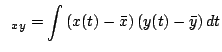 |
(2.21) |
Dzięki temu w przypadku, gdy sygnały są od siebie niezależne,
![]() będzie bliska zeru -- uniezależnia to miarę kowariancji
od wartości średnich sygnałów. Aby otrzymać wartości z przedziału
będzie bliska zeru -- uniezależnia to miarę kowariancji
od wartości średnich sygnałów. Aby otrzymać wartości z przedziału ![]() wprowadzamy jako czynnik normalizacyjny wariancję sygnału:
wprowadzamy jako czynnik normalizacyjny wariancję sygnału:
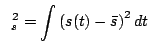 |
(2.22) |
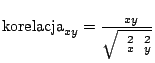 |
(2.23) |
Może się zdarzyć, że dwa sygnały są bardzo podobne, tylko przesunięte
względem siebie w czasie. W wykryciu takiej sytuacji pomaga funkcja
korelacji wzajemnej, czyli korelacja dwóch sygnałów w funkcji
ich wzajemnego przesunięcia. Z kolei autokorelacja to miara korelacji
sygnału ![]() z jego kopią przesuniętą o
z jego kopią przesuniętą o ![]() . Pomijając normalizację
i odejmowanie średnich otrzymamy
. Pomijając normalizację
i odejmowanie średnich otrzymamy
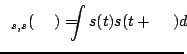 |
(2.24) |
Funkcja autokorelacji będzie miała oczywiście maksimum w zerze, a istnienie innych maksimów związane jest z występowaniem w sygnale okresowo powtarzających się zjawisk. Twierdzenie Wienera-Chinczyna mówi wręcz, że widmo mocy obliczać możemy jako transformatę Fouriera funkcji autokorelacji.
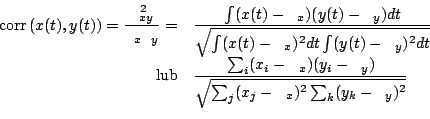 |
(2.25) |
Rozważmy transformatę Fouriera funkcji korelacji sygnałów ![]() i
i ![]() ,
dla uproszczenia pomijając normalizację:
,
dla uproszczenia pomijając normalizację:
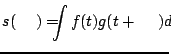 |
(2.26) |
Jak widać, operator korelacji odpowiada w przestrzeni transformat Fouriera iloczynowi transformaty jednego sygnału ze sprzężeniem zespolonym transformaty drugiego.
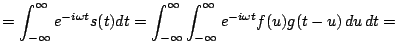 |
|||
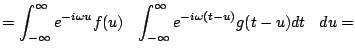 |
|||
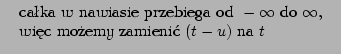 |
|||
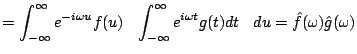 |
transformata Fouriera funkcji autokorelacji jest równa kwadratowi modułu transformaty Fouriera.