




Next: Szereg Fouriera
Up: Klasyczna analiza sygnałów
Previous: Klasyczna analiza sygnałów
Spis tresci
Skorowidz
Systemy liniowe niezmiennicze w czasie (LTI)
Matematycznie system traktować będziemy jako transformację
(operator), przekształcającą sygnał wejściowy 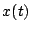 w
w 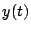 :
Będziemy się zajmować klasą systemów liniowych niezmienniczych w
czasie (ang. Linear Time-Invariant, LTI), działających na
sygnałach dyskretnych, czyli:
:
Będziemy się zajmować klasą systemów liniowych niezmienniczych w
czasie (ang. Linear Time-Invariant, LTI), działających na
sygnałach dyskretnych, czyli:
System 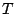 jest liniowy, gdy:
jest liniowy, gdy:
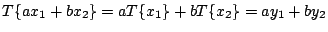 |
(2.1) |
Dla takiego systemu interesujące będzie badanie przekształcenia sekwencji jednostkowej
![$\displaystyle \delta[n]=\left\{ \begin{array}{l} 1 \;\mathrm{dla} \; n=0\\ 0 \;\mathrm{dla} \; n\ne 0 \end{array} \right .$](img99.png) |
(2.2) |
Niech 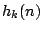 - odpowiedź systemu
- odpowiedź systemu 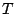 na impuls jednostkowy w punkcie
na impuls jednostkowy w punkcie 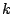 :
:
Każdy dyskretny sygnał 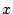 możemy przedstawić jako ważoną sumę sekwencji jednostkowych:
Gdzie
możemy przedstawić jako ważoną sumę sekwencji jednostkowych:
Gdzie ![$ x[k]$](img104.png) , czyli wartość sygnału
, czyli wartość sygnału 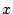 w punkcie k, przyjmuje rolę
liczby mnożącej funkcje
w punkcie k, przyjmuje rolę
liczby mnożącej funkcje
![$ \delta[n-k]$](img105.png) . Jeśli
. Jeśli 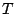 jest systemem liniowym, to
Jeśli system jest niezmienniczy w czasie, to odpowiedź na sekwencję jednostkową
jest systemem liniowym, to
Jeśli system jest niezmienniczy w czasie, to odpowiedź na sekwencję jednostkową
![$ T\{\delta[n-k]\} = h_k[n]$](img107.png) będzie niezależna od
będzie niezależna od 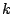 :
:
![$ T\{\delta[n-k]\} = h[n]$](img108.png) . Wtedy
. Wtedy
![$\displaystyle y[n]=\sum_k x[k] h[n-k] = x[n] \star h[n] = h[n] \star x[n] = \sum_k h[k] x[n-k]$](img109.png) |
(2.3) |
gdzie 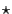 oznacza splot2.3.
Otrzymaliśmy w ten sposób pierwszy ważny wynik:
oznacza splot2.3.
Otrzymaliśmy w ten sposób pierwszy ważny wynik:
Znając odpowiedź systemu liniowego niezmienniczego w czasie na
sekwencję jednostkową, możemy obliczyć jego odpowiedź na dowolny
sygnał. Tak więc funkcja odpowiedzi impulsowej systemu LTI stanowi
jego kompletny opis.
Następnym krokiem w badaniu własności matematycznych przekształceń
bywa poszukiwanie punktów stałych, czyli niezmienników. Rozważmy
przekształcenie LTI wykładniczej funkcji
zespolonej2.4
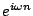 ; z (2.3)
; z (2.3)
![$\displaystyle T\left\{e^{i\omega n}\right\} = \sum_k h[k]\, e^{i\omega (n-k)} = e^{i\omega n} \sum_k h[k]\, e^{-i\omega k}$](img121.png) |
(2.4) |
Przed znak sumy wyciągneliśmy podlegającą transformacji zespoloną
funkcję wykładniczą
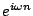 . Wartość sumy
. Wartość sumy
![$ \sum_k
h[k]\,e^{-i\omega k}$](img122.png) zależy od funkcji odpowiedzi impulsowej systemu
zależy od funkcji odpowiedzi impulsowej systemu
![$ h[k]$](img123.png) i częstości
i częstości 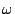 2.5. Tak więc odpowiedź systemu LTI na funkcję
2.5. Tak więc odpowiedź systemu LTI na funkcję
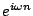 polega na wymnożeniu tej funkcji przez liczbę, czyli
inaczej mówiąc funkcje zespolone od argmentu urojonego są wektorami
własnymi przekstałceń LTI, a odpowiadające im wartości własne to
polega na wymnożeniu tej funkcji przez liczbę, czyli
inaczej mówiąc funkcje zespolone od argmentu urojonego są wektorami
własnymi przekstałceń LTI, a odpowiadające im wartości własne to
![$ \sum_k
h[k]\,e^{-i\omega k}$](img122.png) .
.
Gdybyśmy potrafili dowolną funkcję rozłożyć na sumę zespolonych
funkcji wykładniczych, np. w postaci
działanie systemów LTI ograniczałoby się do łatwo obliczalnych
modyfikacji współczynników 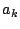 . Następne rozdziały odpowiadają na
pytanie, czy jest to możliwe. Rozważania te będzie łatwiej prowadzić w
przestrzeni funkcji ciągłych, stąd na pewnien czas dyskretny sygnał
. Następne rozdziały odpowiadają na
pytanie, czy jest to możliwe. Rozważania te będzie łatwiej prowadzić w
przestrzeni funkcji ciągłych, stąd na pewnien czas dyskretny sygnał
![$ s[n]$](img87.png) zastąpimy ciągłym
zastąpimy ciągłym 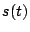 . Zacznijmy od prostszego przypadku
sygnałów okresowych2.6.
. Zacznijmy od prostszego przypadku
sygnałów okresowych2.6.





Next: Szereg Fouriera
Up: Klasyczna analiza sygnałów
Previous: Klasyczna analiza sygnałów
Spis tresci
Skorowidz
Piotr J. Durka
2004-01-05
![]() jest liniowy, gdy:
jest liniowy, gdy:
![$\displaystyle \delta[n]=\left\{ \begin{array}{l} 1 \;\mathrm{dla} \; n=0\\ 0 \;\mathrm{dla} \; n\ne 0 \end{array} \right .$](img99.png)
![]() - odpowiedź systemu
- odpowiedź systemu ![]() na impuls jednostkowy w punkcie
na impuls jednostkowy w punkcie ![]() :
:
![$\displaystyle x[n] = \sum_k x[k] \delta[n-k]
$](img103.png)
![$\displaystyle y[n] = T\left\{ \sum_k x[k]\delta[n-k] \right\} =\sum_k x[k] T\left\{\delta[n-k]\right\} = \sum_k x[k] h_k[n]
$](img106.png)
![]() ; z (2.3)
; z (2.3)
![$\displaystyle s[n] = \sum_k a_k e^{i k n},
$](img124.png)