



Next: Gęstość energii w przestrzeni
Up: Algorytm MP i słowniki
Previous: Algorytm MP i słowniki
Spis rzeczy
Dyskretny słownik funkcji Gabora
Funkcję (atom) słownika czasowo-częstotliwościowego
można wyrazić jako translację (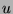 ), rozciągnięcie (
), rozciągnięcie (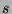 ) i modulację
(
) i modulację
(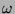 ) funkcji okna
) funkcji okna
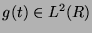
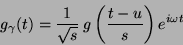 |
(4) |
Optymalną lokalizację w przestrzeni czas-częstość otrzymujemy dla Gaussowskiej
obwiedni 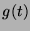 , co w przypadku analizy sygnałów o wartościach rzeczywistych
daje słownik rzeczywistych atomów Gabora:
, co w przypadku analizy sygnałów o wartościach rzeczywistych
daje słownik rzeczywistych atomów Gabora:
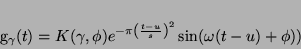 |
(5) |
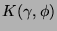 zapewnia normalizację
zapewnia normalizację
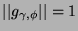 .
Pomimo, że analizujemy sygnały dyskretne, parametry atomów słownika
przyjmować mogą wartości z przedziałów ciągłych. Nawet jeśli w konstrukcji
słownika dla sygnału o danej długości (np. rzędu
.
Pomimo, że analizujemy sygnały dyskretne, parametry atomów słownika
przyjmować mogą wartości z przedziałów ciągłych. Nawet jeśli w konstrukcji
słownika dla sygnału o danej długości (np. rzędu  punktów)
uwzględnimy tylko całkowite wartości parametrów
punktów)
uwzględnimy tylko całkowite wartości parametrów
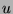 ,
, 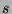 , i
, i 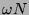 6
z zakresu ,,sensownego'' dla sygnału o danej długości, to i tak otrzymany rozmiar
słownika powoduje ogromny koszt obliczeniowy procedury. W praktyce bardzo
niewiele tracimy korzystając
z relatywnie małego podzbioru przestrzeni (całkowitych) parametrów
6
z zakresu ,,sensownego'' dla sygnału o danej długości, to i tak otrzymany rozmiar
słownika powoduje ogromny koszt obliczeniowy procedury. W praktyce bardzo
niewiele tracimy korzystając
z relatywnie małego podzbioru przestrzeni (całkowitych) parametrów
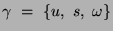 . Tak np. w ,,klasycznej'' implementacji,
zaproponowanej przez autorów metody [7], dla sygnału o długości
. Tak np. w ,,klasycznej'' implementacji,
zaproponowanej przez autorów metody [7], dla sygnału o długości
 punktów
punktów
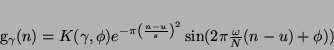 |
(6) |
Wybór parametrów podlega nowemu parametrowi--oktawie 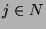 . Skala
. Skala 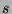 ,
odpowiadająca szerokości atomu w czasie, pochodzi z diadycznej sekwencji
,
odpowiadająca szerokości atomu w czasie, pochodzi z diadycznej sekwencji
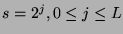 . Parametry
. Parametry 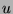 i
i 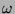 ,
odpowiadające pozycji w czasie i częstości, są próbkowane dla każdej oktawy
z interwałem
,
odpowiadające pozycji w czasie i częstości, są próbkowane dla każdej oktawy
z interwałem  .
.




Next: Gęstość energii w przestrzeni
Up: Algorytm MP i słowniki
Previous: Algorytm MP i słowniki
Spis rzeczy
Piotr J. Durka
1999-09-18