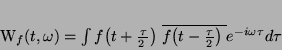Next: Literatura
Up: Algorytm MP i słowniki
Previous: Dyskretny słownik funkcji Gabora
Spis rzeczy
Gęstość energii w przestrzeni czas-częstość
Z definicji transformaty Wignera:
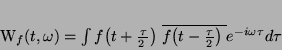 |
(7) |
i reprezentacji (3) możemy skonstruować estymatę gęstości
energii sygnału w przestrzeni czas-częstość [7].
Transformata Wignera równania (3) daje
Podwójna suma zawiera wyrazy mieszane, znacząco fałszujące obraz rozkładu
energii sygnału w klasycznej transformacie Wignera i pochodnych; minimalizacja
ich wkładu w tych rozkładach jest przedmiotem zastosowań zaawansowanych
technik matematycznych.
Dzięki rozkładowi sygnału postaci równania (3), możliwe
jest ich usunięcie explicite--po prostu pomijamy podwójną sumę, definiując
wielkość
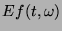 :
:
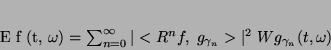 |
(9) |
Dystrybucja Wignera pojedynczego atomu 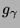 spełnia
spełnia
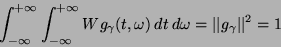 |
(10) |
co w połączeniu z zachowaniem energii rozwinięcia MP
(eq. 3) daje
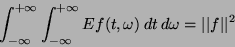 |
(11) |
Uzasadnia to interpretację wielkości 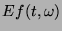 jako gęstości energii
sygnału
jako gęstości energii
sygnału
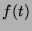 w przestrzeni czas-częstość.
w przestrzeni czas-częstość.




Next: Literatura
Up: Algorytm MP i słowniki
Previous: Dyskretny słownik funkcji Gabora
Spis rzeczy
Piotr J. Durka
1999-09-18