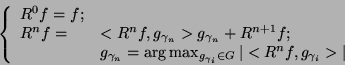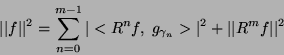Next: Dyskretny słownik funkcji Gabora
Up: Elektroencefalogram i adaptywne aproksymacje
Previous: Właściwości statystyczne dekompozycji
Spis rzeczy
Niech dany będzie (słownik) zbiór funkcji
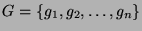 takich, że
takich, że 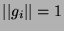 .
Algorytm Matching Pursuit (MP) [7]
jest procedurą iteracyjną. W pierwszym kroku wybierana jest funkcja
.
Algorytm Matching Pursuit (MP) [7]
jest procedurą iteracyjną. W pierwszym kroku wybierana jest funkcja
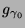 dająca największy iloczyn skalarny z sygnałem
dająca największy iloczyn skalarny z sygnałem
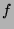 , po czym w każdym następnym kroku funkcja
, po czym w każdym następnym kroku funkcja
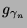 jest analogicznie dopasowywana do residuum sygnału
jest analogicznie dopasowywana do residuum sygnału 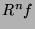 ,
pozostałego po odjęciu wyniku poprzedniej iteracji:
,
pozostałego po odjęciu wyniku poprzedniej iteracji:
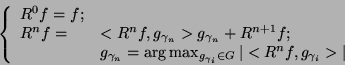 |
(1) |
Ortogonalność 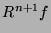 i
i 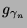 w każdym kroku procedury
implikuje zachowanie energii:
w każdym kroku procedury
implikuje zachowanie energii:
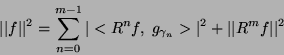 |
(2) |
Jeśli słownik jest kompletny, procedura zbiega do 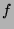 :
:
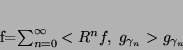 |
(3) |
Subsections
Piotr J. Durka
1999-09-18