Właściwości statystyczne dekompozycji

Zapis EEG jednej nocy w tradycyjnej formie to wstęga papieru długości ok. 0.5 km. Również w analizie zapisów cyfrowych mamy tu do czynienia ze stosunkowo dużą ilością danych. Natrafiliśmy dzięki temu na interesujący problem, wynikający z własności statystycznych procedury MP. Używane w praktyce słowniki czasowo-częstotliwościowe stanowią dość rzadki podzbiór przestrzeni dopuszczalnych parametrów funkcji Gabora. W szczególności, zaproponowana przez autorów metody implementacja [7] oparta jest o diadyczny (oparty na potęgach dwójki) schemat wyboru parametrów (patrz Dodatek A.1). 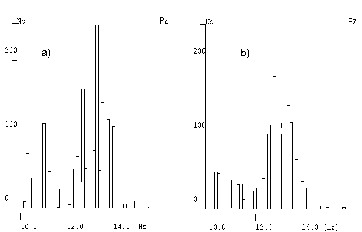Rysunek 7a (lewy panel) przedstawia histogram częstości wrzecion snu wybranych z dekompozycji EEG w takim właśnie diadycznym słowniku. Poza szerokim pikiem w okolicy 13 Hz widać w histogramie subtelną strukturę, której powtarzalność mogłaby sugerować np. preferencję mózgu dla pewnych częstości. Jest to jednak artefakt metody, związany z faktem, że w użytym słowniku w okolicy tychże częstości znajduje się więcej atomów o zbliżonych parametrach. Prowadzi to do powstania swego rodzaju atraktora dla dekompozycji, którego efekt ujawnia się w sensie statystycznym dopiero przy analizie większej ilości danych.

Rysunek 7: Histogram częstości wrzecion wybranych z dekompozycji całonocnego zapisu EEG, uzyskanej z pomocą a) słownika diadycznego, b) słowników stochatycznych

W tym miejscu pojawia się interesujące pytanie: jeśli diadyczny schemat próbkowania przestrzeni parametrów słownika powoduje tego typu artefakty, to jaki jest ,,właściwy'' schemat ich wyboru, dający nieobciążone statystycznie wyniki? Niestety każdy ustalony schemat będzie wpływał na statystykę wyników. Pozostaje zdać się na ...przypadek, i losować parametry atomów słownika przed każdą dekompozycją. Taką właśnie procedurę wprowadziliśmy pod nazwą słowników stochastycznych. Wynik jej działania ilustruje rysunek 7b. Poprawne właściwości statystyczne uzyskujemy kosztem większej ilości obliczeń, gdyż musimy w tej sytuacji zrezygnować z optymalizacji numerycznych związanych ze szczególną strukturą słownika. Opisana powyżej metoda może otworzyć nowe możliwości w analizie sygnałów niestacjonarnych również z innych dziedzin. Zainteresowanych powyższą tematyką zapraszam na stronę http://durka.info, gdzie znaleźć można m. in. interaktywne programy demonstrujące wyniki rozkładu MP.