Reprezentacja sygnału w redundantnym zbiorze funkcji

Zrozumieć w kulturze europejskiej znaczy często powiedzieć własnymi słowami. Podobnie analiza funkcji polegać może na jej przedstawieniu--lub przybliżeniu--z pomocą funkcji o znanych właściwościach. Kontynuując tę analogię, zbiór znanych funkcji, z pomocą których będziemy chcieli wytłumaczyć funkcję nieznaną, nazwiemy słownikiem. Szczególnym przypadkiem słownika jest baza ortogonalna--najmniejszy kompletny słownik. Z pomocą niewielu prostych i podstawowych słów można wytłumaczyć niemal dowolnie skomplikowane idee. Jednak opis z użyciem ubogiego słownika nie będzie zwięzły ani elegancki. Dla trafnego wyrażenia subtelnych i nieuchwytnych idei--bądź słabych i przejściowych składowych sygnału--potrzebujemy obszerniejszego słownika, wzbogaconego o wyrażenia fachowe lub licencję poetycką. W analizie sygnałów słownik możemy rozszerzać niemal dowolnie--wystarczy sparametryzować ogólną postać funkcji składowych (przykładowy słownik opisany jest w Dodatku). Dokładny opis sygnału (tj. badanej funkcji) w słowniku większym niż baza wprowadza redundancję. Zwięzłość osiągnąć możemy godząc się na przybliżenie sygnału, ale za to z pomocą możliwie niewielkiej ilości funkcji. Jeśli ilość wybranych do reprezentacji sygnału funkcji słownika nazwiemy rozmiarem reprezentacji, to dążyć będziemy zwykle do sytuacji, w której:

rozmiar reprezentacji$<$wymiar bazy$<<$rozmiar słownika

Reprezentację optymalną możemy określić jako taki podzbiór elementów słownika, którego liniowa kombinacja tłumaczy największy procent energii sygnału wśród wszystkich podzbiorów o tej samej liczebności. Wybór takiej reprezentacji jest obliczeniowo NP-trudny², toteż w praktyce zadowalamy się iteracyjnym rozwiązaniem sub-optymalnym--zaproponowanym w 1993 przez S. Mallata i Z. Zhanga [7] algorytmem Matching Pursuit (MP).

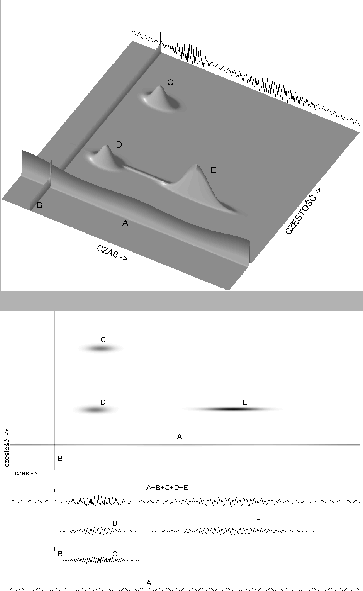
Rysunek 4: Uzyskana z rozkładu MP gęstość energii w przestrzeni czas-częstość sygnału symulowanego jako suma sinusa (A), delty Diraca (B) i trzech funkcji Gabora o parami jednakowych położeniach w czasie (C i D) i częstościach (D i E).

W analizie sygnałów używamy zwykle słowników złożonych z funkcji Gabora (Gauss modulowany sinusem) ze względu na ich optymalną lokalizację w przestrzeni czas-częstość. Reprezentacja złożona z funkcji Gabora pozwala również na konstrukcję eleganckiej estymaty gęstości energii sygnału w przestrzeni czas-częstość, usuwającej a priori problem wyrazów mieszanych obecny w tego typu dystrybucjach (patrz Dodatek A.2).

Rysunek 5: Dekompozycja sygnału z rys. 4 z liniowym dodatkiem szumu o dwukrotnie większej energii 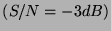$(S/N = -3 dB)$

Wynik działania algorytmu ze słownikiem funkcji Gabora przedstawia rysunek 4; sygnał zasymulowano jako sumę sinusa, delty Diraca (jednopunktowej nieciągłości) i trzech funkcji Gabora o parami jednakowych położeniach w czasie i częstościach. Rysunek 5 przedstawia dekompozycję tegoż sygnału z dodanym liniowo szumem o dwukrotnie większej energii.