

Next: Discussion
Up: Results
Previous: Classical results
Average time-frequency maps of energy density of EEG responses
(Figures 5, 6) were obtained as
follows:
- Single trials from the data described in chapter 2 were
subjected to MP decomposition in stochastic Gabor dictionaries.
- For each trial, a time-frequency map of signal's energy density was
constructed. Time-frequency structures of duration below 0.125
sec. were excluded from the maps--this can be understood as a kind of
non-linear denoising, and corresponds to smoothing in time curves from
Figure 3 by 16-points window. Parallel procedure (exclusion
of structures longer than 4 sec.) was used to remove sharp frequency
artifacts.
- Finally, all the time-frequency maps constructed for single trials
were added, to produce an average (across trials) distribution of
signal's energy in the time-frequency plane (Figures
5 and 6).
Slices corresponding to the frequency bands used in classical ERD/ERS
quantification (section 3.1) were cut from this
distribution in Figure 4. Curves presented above those
slices are corresponding frequency integrals. Value at each point of a
curve is a sum of energies at this time point for all the frequencies
in given band, i.e. from the the map below.
Figure 4:
Average time-frequency maps of EEG energy density, obtained
from the same data as analyzed in Figure 3. Horizontal
axis--time in seconds relative to the finger movement. Vertical axes
on the right of those maps indicate frequency in Hz. Energy
proportional to shades of gray. Scale is arbitrary and different for
each map. Curves above the maps, corresponding to figure
3, are frequency integrals of the maps below
them. Vertical axes on their left sides indicate percent of change,
relative to energy integrated between 3.5 and 4.5 seconds before the
movement in given band.
|
|
Figure 5:
Complete time-frequency map (from 5 to 40 Hz), from which
slices presented in Figure 4 were cut. Horizontal
scale--seconds relative to the finger movement, vertical--frequency
(Hz). Top--the same in 3 dimensions, but energy of the alpha band cut
off in 50% of the height to show weaker high-frequency
structures. Presentation as in Figure 1.
|
|
Figure 6:
The same as Fig. 5, calculated for referential data.
Alpha band energy in the 3-D plot cut at 25%.
|
|
Parametric description of signal structures opens also amazing
possibilities of signal analysis in the space of parameters of
functions from the signal's expansion (3). As an
example, Figure 7 presents estimation of the energy
carried by structures with frequency centers lying within certain
interval--as opposed to the energy calculated as an integral of the
spectral power within the same interval or energy of band-pass
filtered signals. Difference between those estimates is explained in
Figure 8. Choice of the gamma band between 35 and 38
Hz, based upon the overall picture from Figure 5,
combined with such a selective energy estimate, increased the
estimated gamma ERS above 4000%--double the result obtained via
integration of the overall MP estimate between 36 and 40 Hz
(Fig. 4).6
Figure 7:
Bottom: time-frequency distribution of energy carried by structures
with frequency centers lying between 35 and 38 Hz (interval chosen from
the full picture of energy changes displayed in Figure
5). Top: gamma ERS based upon this estimate.
Presentation as in Figure 4.
|
|
Figure 8:
Difference between the spectral integral from 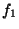 to
to 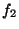 and the
actual power carried by structures with frequency centers lying within
this interval. Black solid line--spectrum resulting from the presence
of three structures (spectra plotted with dotted and dashed lines in
(a)). (b)--the actual power carried by the structure with
frequency center between
and the
actual power carried by structures with frequency centers lying within
this interval. Black solid line--spectrum resulting from the presence
of three structures (spectra plotted with dotted and dashed lines in
(a)). (b)--the actual power carried by the structure with
frequency center between 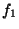 and
and 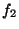 (dark gray), (c)--spectral integral from
(dark gray), (c)--spectral integral from 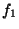 to
to  . We observe that part of
the energy originating within the interval spreads outside it, while
part of energy of structures originating at outside frequencies
contributes to the power integrated within the interval. Method
proposed in this paper offers estimate corresponding to the dark area
in (b). On the contrary, the classical estimate obtained via band-pass
filtering is a smeared version of the light gray area in (c), since the
band-pass properties of a filter are never perfect.
. We observe that part of
the energy originating within the interval spreads outside it, while
part of energy of structures originating at outside frequencies
contributes to the power integrated within the interval. Method
proposed in this paper offers estimate corresponding to the dark area
in (b). On the contrary, the classical estimate obtained via band-pass
filtering is a smeared version of the light gray area in (c), since the
band-pass properties of a filter are never perfect.
|
|
Footnotes
- ...fig:local).6
- These numbers are quoted here only to
illustrate the increase of sensitivity; per se they do not provide
direct measures of the underlying phenomena. If we assume a complete
absence of gamma in the reference period, their theoretical value would
be infinite.


Next: Discussion
Up: Results
Previous: Classical results
Piotr J. Durka
2001-03-23
![\includegraphics[width=8cm]{figures/fig04.eps}](img31.png)
![\includegraphics[width=8cm]{figures/fig04.eps}](img31.png)
![\includegraphics[width=\columnwidth]{figures/fig05.eps}](img32.png)
![\includegraphics[width=\columnwidth]{figures/fig06.eps}](img33.png)
![\includegraphics[width=8cm]{figures/fig07.eps}](img34.png)
![\includegraphics[width=6cm]{figures/fig08.eps}](img35.png)