- Reference epoch
- Permutation test on the difference of means
- Bootstrap with pseudo-
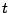 statistics
statistics
- Computational complexity
- Adjustment for multiplicity
The two methods discussed below represent the extrema of the wide spectrum of possible time-frequency estimators: spectrogram offers a fast algorithm and well established properties, while MP has the highest presently available resolution at a cost of a high computational complexity. Both these methods offer uniform time-frequency resolution, as opposed to the time-scale approaches (wavelets).
Short time Fourier transform (STFT or spectrogram) divides the signal into overlapping epochs. Each of these epochs is multiplied by a window function and then subjected to the Fast Fourier Transform [12], providing spectrum with resolution dependent on the epoch's length. We used Hanning windows with overlap 1/2 of its length.
Dictionaries (![]() ) for time-frequency analysis of real signals
are constructed from real Gabor functions:
) for time-frequency analysis of real signals
are constructed from real Gabor functions:
![]() is the size of the signal,
is the size of the signal,
![]() is such that
is such that
![]() ,
,
![]() denotes parameters of the dictionary's functions. For these
parameters no particular sampling is a priori defined. In practical
implementations we use subsets of the infinite space of possible dictionary's
functions.
However, any fixed scheme of subsampling this space introduces a statistical bias
in the resulting parametrization. In [14] we proposed a solution in
terms of MP with stochastic dictionaries, where the parameters of a
dictionary's atoms are randomized before each decomposition, or drawn from flat
distributions. Results presented in this paper were obtained with such a bias-free
implementation.
denotes parameters of the dictionary's functions. For these
parameters no particular sampling is a priori defined. In practical
implementations we use subsets of the infinite space of possible dictionary's
functions.
However, any fixed scheme of subsampling this space introduces a statistical bias
in the resulting parametrization. In [14] we proposed a solution in
terms of MP with stochastic dictionaries, where the parameters of a
dictionary's atoms are randomized before each decomposition, or drawn from flat
distributions. Results presented in this paper were obtained with such a bias-free
implementation.
For a complete dictionary the procedure converges to ![]() , but in
practice we use finite sums:
, but in
practice we use finite sums:
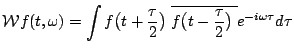 |
(4) |
calculated for the expansion (3). This representation will be a priori free of cross-terms:
Time-frequency resolution of signal's representation depends on a
multitude of factors, which are even more complicated in the case of
the averaged estimates of energy. A general lower bound is given by
the uncertainty principle, which states (c.f. [15]) that the
product of the time and frequency variances exceeds a constant, which
for the frequency defined as inverse of the period (Hz)![]() equals to
equals to
![]() :
:
It can be proved that equality in this equation is achieved by
complex Gabor functions; other functions give higher values of this
product. Since the time and frequency spreads are proportional to the
square root of the corresponding variances, minimum of their product
reaches
![]() .
.
However, our attempts to estimate the statistical significance in
small resels of area given by (6) resulted in increased "noise",
i.e., detections of isolated changes in positions inconsistent across
varying other parameters. Therefore we fixed the area of resels at
![]() , which at least has certain statistical justification:
standard, generally used sampling of the spectrogram gives
, which at least has certain statistical justification:
standard, generally used sampling of the spectrogram gives ![]() as the product of the localization in time (window length less overlap) and in
frequency (interval between estimated frequencies). This sampling is
based upon statistically optimal properties, namely independent samples
for a periodogram of a Gaussian random process (c.f. [16]).
Other values of this parameter can be of course considered in
practical applications: the software accompanying this paper
allows to investigate the impact of changing this parameter.
as the product of the localization in time (window length less overlap) and in
frequency (interval between estimated frequencies). This sampling is
based upon statistically optimal properties, namely independent samples
for a periodogram of a Gaussian random process (c.f. [16]).
Other values of this parameter can be of course considered in
practical applications: the software accompanying this paper
allows to investigate the impact of changing this parameter.
Unlike the spectrogram (STFT, section II-A.1), MP decomposition
(section II-A.2) generates a continuous map of the energy density
(5). From this decomposition a discrete map must be
calculated with a finite resolution. The simplest solution is to sum
for each resel the values of all the functions from the
expansion![]() (3) in
the center of each resel (
(3) in
the center of each resel (
![]() ):
):
However, for certain structures or relatively large resels, (7) may not be representative for the amount of energy contained in given resel. Therefore we use the exact solution, obtained by integrating for each resel power of all the functions from expansion (3) within the ranges corresponding to the resel's boundaries:
The difference between (7) and (8) is most significant for structures narrow in time or frequency relative to the dimensions of resels. In this study we used relatively large resel's area and the average difference in energy did not exceed 5-7%.
Strict assumption of stationarity of the signals in the reference epoch
would make an elegant derivation of the applied statistics: the
repetitions could be then treated as realizations of an ergodic
process. Indeed, epochs of EEG up to 10 sec duration (recorded under
constant behavioral conditions) are usually considered stationary
[17]. However, the assumption of ``constant behavioral
conditions'' can be probably challenged in some cases. We cannot test
this assumption directly, since the usual length of the reference
epoch is too short for a standard test of
stationarity.![]() Nevertheless, bootstrapping the available data across the indexes
corresponding to time
and repetition (number of the trial) simultaneously
does not require a strict assumption of ergodicity from the purely
statistical point of view. But we must be aware that this fact does
not diminish our responsability in the choice of the reference epoch,
which in general should be long enough to represent the ``reference''
properties of the signal to which the changes will be related, and at
the same time it should be distant enough from the beginning of the
recorded epoch (to avoid the influence of border conditions in
analysis) and the investigated phenomenon (not to include some
event-related properties in the ``reference'').
Nevertheless, bootstrapping the available data across the indexes
corresponding to time
and repetition (number of the trial) simultaneously
does not require a strict assumption of ergodicity from the purely
statistical point of view. But we must be aware that this fact does
not diminish our responsability in the choice of the reference epoch,
which in general should be long enough to represent the ``reference''
properties of the signal to which the changes will be related, and at
the same time it should be distant enough from the beginning of the
recorded epoch (to avoid the influence of border conditions in
analysis) and the investigated phenomenon (not to include some
event-related properties in the ``reference'').
The values of energy of all the ![]() repetitions in each questioned resel
will be compared to energies of resels within the
corresponding frequency of the reference epoch.
Lets denote the time indexes
repetitions in each questioned resel
will be compared to energies of resels within the
corresponding frequency of the reference epoch.
Lets denote the time indexes ![]() of resels belonging to the
reference epoch as
of resels belonging to the
reference epoch as
![]() and their number
contained in each frequency slice (defined by the frequency width of
a resel) as
and their number
contained in each frequency slice (defined by the frequency width of
a resel) as
![]()
![]() . We have a total of
. We have a total of ![]() repetitions of signals and their
time-frequency maps. So for each frequency we have a total of
repetitions of signals and their
time-frequency maps. So for each frequency we have a total of
![]() values of energy in the corresponding
resels.
For each resel at coordinates
values of energy in the corresponding
resels.
For each resel at coordinates
![]() we'll compare its
energy averaged over
we'll compare its
energy averaged over ![]() repetitions with the energy averaged over
repetitions in resels from the reference epoch in the same frequency.
Their difference can be written as:
repetitions with the energy averaged over
repetitions in resels from the reference epoch in the same frequency.
Their difference can be written as:
The values of
![]() tend to have
(especially for the MP estimates) a highly non-normal distributions.
It is caused mainly by the adaptivity and high resolution of the MP
approximation. Namely, the areas where no coherent signal's structures
are encountered by the algorithm are left completely ``blank", which
causes the appearance of peaks around zero in histograms presented in Figure
1.
On the contrary, other estimates of energy density provide a more uniform filling of the time-frequency plane, because of lower resolution and cross-terms.
tend to have
(especially for the MP estimates) a highly non-normal distributions.
It is caused mainly by the adaptivity and high resolution of the MP
approximation. Namely, the areas where no coherent signal's structures
are encountered by the algorithm are left completely ``blank", which
causes the appearance of peaks around zero in histograms presented in Figure
1.
On the contrary, other estimates of energy density provide a more uniform filling of the time-frequency plane, because of lower resolution and cross-terms.
Given these distributions, we cannot justify an application of a parametric test based upon the assumption of normality. In order to preserve high power of the test we estimate the distributions from the data themselves by means of resampling methods (c.f. [19]).
![\includegraphics[width=.44\textwidth]{fig/hist.eps}](img43.png)
|
We are testing the null hypothesis of no difference in means between
the values
![]() of
the
of
the ![]() -th resel and all those in corresponding reference region
-th resel and all those in corresponding reference region
![]() , that is energy values for the same frequency band for the resels falling into the reference epochs in all the repetitions (trials). A straightforward application of the idea of the
permutation tests for each resel consists of:
, that is energy values for the same frequency band for the resels falling into the reference epochs in all the repetitions (trials). A straightforward application of the idea of the
permutation tests for each resel consists of:
The number of permutations giving values of (9) exceeding
the observed value has a binomial distribution for
![]() repetitions with probability
repetitions with probability ![]() .
.![]() Its variance equals
Its variance equals
![]() .
The relative error of
.
The relative error of ![]() will be then (c.f. [19])
will be then (c.f. [19])
To keep this relative error at 10% for a significance level
![]() =5%,
=5%,
![]() is enough. Unfortunately, due to
the problem of multiple comparisons discussed in Section
II-D.5, we need to work with much smaller values of
is enough. Unfortunately, due to
the problem of multiple comparisons discussed in Section
II-D.5, we need to work with much smaller values of
![]() . In this study
. In this study
![]() was set to
was set to
![]() or
or
![]() , which resulted in large computation times. Therefore we
implemented also a less computationally demanding approach, described
in the following section.
, which resulted in large computation times. Therefore we
implemented also a less computationally demanding approach, described
in the following section.
Where
![]() is defined as in Eq. (9),
and
is defined as in Eq. (9),
and ![]() is the pooled variance of the reference epoch and
the investigated resel.
We estimate the distribution of this magnitude from the data in the
reference epoch (for each frequency
is the pooled variance of the reference epoch and
the investigated resel.
We estimate the distribution of this magnitude from the data in the
reference epoch (for each frequency
![]() values)
by drawing with replacement two samples of sizes
values)
by drawing with replacement two samples of sizes ![]() and
and
![]() and calculating for each such replication statistics (11).
This distribution is
approximated once for each frequency. Then for each resel the actual
value of (11) is compared to this distribution yielding
and calculating for each such replication statistics (11).
This distribution is
approximated once for each frequency. Then for each resel the actual
value of (11) is compared to this distribution yielding ![]() for the null hypothesis.
for the null hypothesis.
Both presented above methods are computer-intensive, which nowadays
causes no problems in standard applications. However, corrections for
multiple comparisons imply much lower effective values of cutoff
probabilities ![]() (see the next section II-D.5). For the analysis presented in
this study both the FDR (False Discovery Rate, see next section)
and Bonferroni-Holmes adjustments gave
critical values of the order of
(see the next section II-D.5). For the analysis presented in
this study both the FDR (False Discovery Rate, see next section)
and Bonferroni-Holmes adjustments gave
critical values of the order of
![]() for the Dataset II
(larger number of investigated resels, see section II-E ``Experimental Data'') and
for the Dataset II
(larger number of investigated resels, see section II-E ``Experimental Data'') and
![]() for
Dataset I. If we set this for
for
Dataset I. If we set this for ![]() in eq. (10), we
obtain minimum of
in eq. (10), we
obtain minimum of
![]() or
or
![]() bootstrap or resampling repetitions to achieve 10% relative error
for
bootstrap or resampling repetitions to achieve 10% relative error
for ![]() .
.
Comparisons on presented datasets confirmed very similar results for
both these procedures, as expected from the discussion in section
II-D.3. This served as a justification to use in practice the
pseudo-![]() bootstrapping, which is
significantly faster.
bootstrapping, which is
significantly faster.![]()
In the preceding two sections we estimated the achieved significance
levels ![]() for a null hypotheses of no change of the average energy
in a single resel compared to the reference region in the same
frequency. Statistics of these tests for different resels are not
independent--neither in the time nor in the frequency dimension, and
the structure of their correlation is hard to guess a priori.
for a null hypotheses of no change of the average energy
in a single resel compared to the reference region in the same
frequency. Statistics of these tests for different resels are not
independent--neither in the time nor in the frequency dimension, and
the structure of their correlation is hard to guess a priori.
Adjusting results for multiplicity is a very important issue in case
of such a large amount of potentially correlated tests. We chose
for this step the procedure assessing the False Discovery Rate (FDR,
proposed in [20]). Unlike the adjustments for the family-wise
error rate (FWE), it controls the ratio ![]() of the number of the true null
hypotheses rejected to all the rejected hypotheses. In our case this
is the ratio of the number of resels to which significant changes are
wrongly attributed to the total number of resels revealing changes.
of the number of the true null
hypotheses rejected to all the rejected hypotheses. In our case this
is the ratio of the number of resels to which significant changes are
wrongly attributed to the total number of resels revealing changes.
The main result presented in [20] requires the test statistics
to have positive regression dependency on each of the test statistics
corresponding to the true null hypothesis. We use a slightly more
conservative version, which controls FDR for all other forms of
dependency. Let's denote the total number of performed tests, equal
to the number of questioned resels, as ![]() . If for
. If for ![]() of them the
null hypothesis of no change is true, [20] proves that the
following procedure controls the FDR at the level
of them the
null hypothesis of no change is true, [20] proves that the
following procedure controls the FDR at the level
![]() :
:
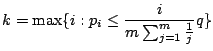 |
(12) |
Another, more conservative correction for multiplicity is the
step-down Bonferroni-Holmes adjustment [11]. It relies on
comparing the ![]() values, ordered as in point (1.) above, to
values, ordered as in point (1.) above, to
![]() , where
, where ![]() controls the family-wise
error. We used
controls the family-wise
error. We used
![]() , which for the FDR relates
to the possibility of erroneous detection of changes in one out of
20 resels indicated as significant.
, which for the FDR relates
to the possibility of erroneous detection of changes in one out of
20 resels indicated as significant.
According to the comparisons performed on the two discussed datasets, false discovery rate (FDR) resulted--as expected--to be less conservative that the stepdown Bonferroni-Holmes procedure. It has also a more appealing interpretation than the family-wise error (FWE) of Bonferroni-like procedures. Both these procedures take negligible amounts of computations.
EEG was registered from electrodes placed at positions selected from the extended 10-20 system, sampled at 256 Hz, analog bandpass filtered in the 0.5-100 Hz range and sub-sampled offline to 128 Hz. For data processing, EEG was divided into 8 seconds long epochs, with movement onset in the 5th second. We present analysis of 57 artifact-free trials of right hand finger movement from the electrode C1 referenced to Cp1, Fc1, Cz and C3 (local average reference).
EEG was registered from electrodes at positions selected from the 10-20 system. For the analysis we choose the C4 electrode (contra-lateral to the hand performing movements) in the local average reference. Analog filters were 100-Hz low-pass and 50-Hz notch. Signal was sampled at 250 Hz and down-sampled offline to 125 Hz.