


Next: Study of C1s [0].
Up: GT resonances from generalized
Previous: GT resonances from generalized
We begin with the simplest case, assuming that
(i) the functional is gauge invariant,
(ii) all time-odd coupling constants are density-independent, and
(iii) the spin-surface term can be neglected, i.e.,
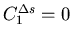 .
The only remaining free parameter in the spin-isospin channel
is C1s, which is directly related to the Landau parameters
via Eqs. (16) and (18):
.
The only remaining free parameter in the spin-isospin channel
is C1s, which is directly related to the Landau parameters
via Eqs. (16) and (18):
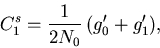 |
(19) |
where g1' is fixed by C1T [also in Eq. (18)].
Figure 6 shows results for the GT resonance energy when
g0' is systematically varied from its SkO' value by altering C1s.
We have chosen only nuclei that can be expected to exhibit a collective
response to GT excitations. Non-collective contributions may show up,
however, when the coupling constants are changed. In 124Sn,
for example, a state below the resonance collects a lot of strength for
small values of g0'. Only by increasing g0' does one push that
strength into the resonance. Similarly, in 112Sn a
state about 5MeV above the resonance increasingly collects
strength as g0' grows.
As the underlying single-particle spectra are the same for all the cases
in Fig. 6, the differences are due entirely to the
value of g0'. With increasing g0', the resonance energy increases
and more strength is pushed into the resonance. The increase of 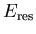 is nearly linear, but the lines for different nuclei have
different slopes. It is gratifying that the curves for
is nearly linear, but the lines for different nuclei have
different slopes. It is gratifying that the curves for
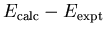 all have a zero around the same point,
all have a zero around the same point,
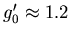 .
This value is much smaller than the
empirical value
.
This value is much smaller than the
empirical value
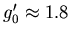 derived earlier
[63,51,52] for at least two reasons: (i) the
influence of the single-particle spectrum, and (ii) the
inclusion in the residual interaction of a p-wave force characterized
by g1'. The latter means that g0'=0 does not correspond to
a vanishing interaction in the spin-isospin channel.
derived earlier
[63,51,52] for at least two reasons: (i) the
influence of the single-particle spectrum, and (ii) the
inclusion in the residual interaction of a p-wave force characterized
by g1'. The latter means that g0'=0 does not correspond to
a vanishing interaction in the spin-isospin channel.
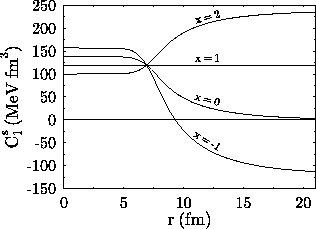
Figure 7:
Spatial dependence of
![$C_1^{s} [\rho]$](img104.png) for various values
of x
for various values
of x C1s[0]/
C1s[0]/
![$C_1^{s} [\rho _{\rm nm}]$](img1.png) ,
cf. Eq. (10), and g0' fixed at 1.2. The value
x=1 corresponds to no density dependence. For larger values
of x, the residual interaction becomes more repulsive outside
the nucleus than inside. When x=0,
,
cf. Eq. (10), and g0' fixed at 1.2. The value
x=1 corresponds to no density dependence. For larger values
of x, the residual interaction becomes more repulsive outside
the nucleus than inside. When x=0, ![$C_1^{s} [\rho]$](img104.png) vanishes
at large distances, and for negative values of x, the residual
interaction becomes attractive outside the nucleus. The density profile
vanishes
at large distances, and for negative values of x, the residual
interaction becomes attractive outside the nucleus. The density profile
 used in this plot corresponds
to 208Pb.
used in this plot corresponds
to 208Pb.
 |



Next: Study of C1s [0].
Up: GT resonances from generalized
Previous: GT resonances from generalized
Jacek Dobaczewski
2002-03-15
![]() is nearly linear, but the lines for different nuclei have
different slopes. It is gratifying that the curves for
is nearly linear, but the lines for different nuclei have
different slopes. It is gratifying that the curves for
![]() all have a zero around the same point,
all have a zero around the same point,
![]() .
This value is much smaller than the
empirical value
.
This value is much smaller than the
empirical value
![]() derived earlier
[63,51,52] for at least two reasons: (i) the
influence of the single-particle spectrum, and (ii) the
inclusion in the residual interaction of a p-wave force characterized
by g1'. The latter means that g0'=0 does not correspond to
a vanishing interaction in the spin-isospin channel.
derived earlier
[63,51,52] for at least two reasons: (i) the
influence of the single-particle spectrum, and (ii) the
inclusion in the residual interaction of a p-wave force characterized
by g1'. The latter means that g0'=0 does not correspond to
a vanishing interaction in the spin-isospin channel.
