GT strength distributions from existing Skyrme interactions

Before exploring the time-odd degrees of freedom of the generalized Skyrme energy functional, we analyze the performance of existing parameterizations when relations (34) are used. We examine the forces SkP [19], SGII [38], SLy4, SLy5 [24], SkO, and SkO'[58], which all provide a good description of ground-state properties but differ in details. SkP uses an effective mass m^*/m = 1 and is designed to describe both the mean-field and pairing effects<¹. All other forces have smaller effective masses, so that $m^*/m \approx 0.9$ (SkOx) or even $m^*/m \approx 0.7$ (SGII, SLyx). SGII represents an early attempt to get good GT response properties from a standard Skyrme force. SLy4 and SLy5 are attempts to reproduce properties of pure neutron matter together with those of normal nuclear ground states. SkO and SkO' are recent fits that include data from exotic nuclei, with particular emphasis on isovector trends in neutron-rich Pb isotopes; they complement the spin-orbit interaction with an explicit isovector degree-of-freedom [42]. All other parameterizations use the standard prescription $C_0^{\nabla J} = 3 C_1^{\nabla J}$.

Residual interactions are often summarized by the Landau parameters that appear in Eq. (13). The parameters can be derived as the corresponding coupling constants when Eq. (14) is evaluated for infinite spin-saturated symmetric nuclear matter (see Appendix 10). In the literature, the infinite nuclear matter (INM) properties of the Skyrme interactions are usually calculated from Eqs. (34). For the generalized energy functional (12) discussed here, the time-even INM properties such as the saturation density, energy per particle, effective mass, incompressibility, symmetry coefficient, and the time-even Landau parameters f_i, f_i' are unchanged, but properties of polarized INM and expressions for the time-odd Landau parameters g_i and g_i' are different. We derive them in Appendix 10. Here we are most concerned with the Landau parameters in the spin and spin-isospin channels,

$$N_0 \big( 2 C_0^{s} + 2 C_0^{T} \, \beta \, \rho_0^{2/3} \big),$$ g₀ = (15)

$$N_0 \big( 2 C_1^{s} + 2 C_1^{T} \, \beta \, \rho_0^{2/3} \big),$$ g₀' = (16)

$$- 2 N_0 \; C_0^{T} \, \beta \, \rho_0^{2/3},$$ g₁ = (17)

$$- 2 N_0 \; C_1^{T} \, \beta \, \rho_0^{2/3},$$ g₁' = (18)

Figure 1: Summed GT strength in ²⁰⁸Pb calculated with several Skyrme interactions, each corresponding to the Landau parameters g₀' and g₁' as indicated. The experimental resonance energy, taken from Ref. [46], is indicated by an arrow.
Figure 2: Same as in Fig. 1 except for ¹²⁴Sn.

where N₀ is given by (69) and $\beta = ( 3 \pi^2 / 2 )^{2/3}$. Values for some typical Skyrme interactions appear in Table 1. Higher-order Landau parameters are zero for the Skyrme functional (12). Some of these values differ from those given elsewhere because, unlike other authors, we insist on exactly the same effective interaction in the HFB and QRPA. The coupling constants C^T₀ and C^T₁ are fixed by the gauge invariance of the energy functional, which means that C^T₁ = 0 for SGII, SLy4 and SkO, because the $\stackrel{\leftrightarrow}{J}^2$ term was omitted in the corresponding mean-field fits. For these interactions g₁' = 0 and $g_0' \approx 0.9$. For SkP and SLy5, and SLy7, C₁^T is relatively large (see Table 4), leading to a large $g_1' \approx 1.0$, but a cancellation between two terms makes $g_0' \approx 0.0$.

Figure 3: Deviation of the calculated GT resonance energy from experiment, $E_{\rm calc} - E_{\rm expt}$, and fraction of the GT strength in the resonance, $B_{\rm res}/B_{\rm tot}$, versus Landau parameter g₀', calculated for several Skyrme interactions (as indicated in the lower right panel) in ⁹⁰Zr, ¹¹²Sn, ¹²⁴Sn, and ²⁰⁸Pb. Experimental values are taken from Ref. [46].

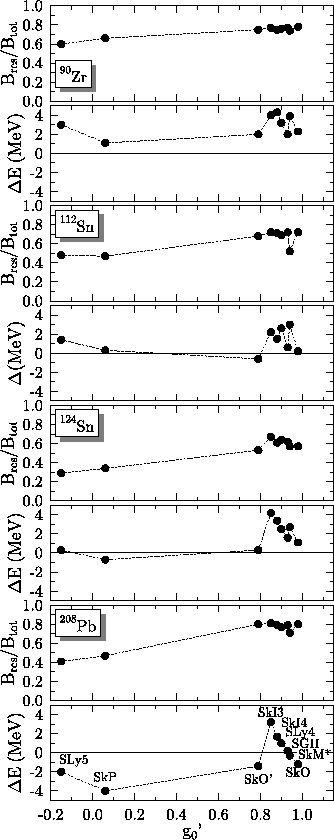Table 1 also gives values for the Landau parameters calculated for the Gogny forces D1 [59] and D1s [22] from the expressions provided in Appendix 11. In the spirit of the Gogny force as a two-body potential, one has no freedom to choose the time-odd terms independently from the time-even ones. (Note that the Gogny force, however, employs the same local-density approximation for the density-dependence as the Skyrme energy functional that contributes to the $\ell = 0$ Landau parameters.) The higher-order Landau parameters are uniquely fixed by the finite-range part of the Gogny force.

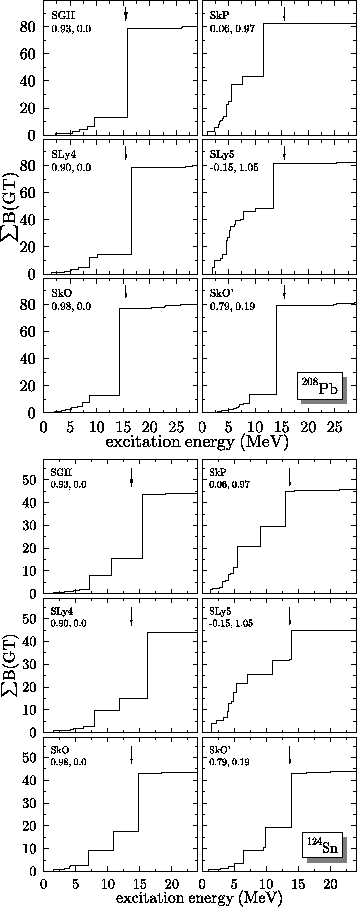
Figures 1 and 2 show the summed GT strength B(GT) in ²⁰⁸Pb and ¹²⁴Sn, calculated with all the selected Skyrme forces. The ground-state energies are calculated as described in Ref. [11], and all strengths are divided by 1.26², following common practice, to account for GT quenching. Although the GT resonance in ²⁰⁸Pb comes out at about the right energy for SGII, SLy4, SkO, and SkO', it is too low for SkP and SLy5. These latter two interactions also leave too much GT strength at small excitation energies. It is tempting to interpret these findings in terms of the Landau parameters for these interactions. Schematic models suggest [1] that an increase of g₀' results in an increased resonance energy and more GT strength in the resonance. The nucleus ²⁰⁸Pb indeed behaves in this way, as can be seen in Fig. 1. The forces SkP and SLy5, with small values of g₀', yield more low-lying strength and a lower resonance energy than the remaining forces which correspond to $g_0' \approx 0.9$.

Figure 4: Same as in Fig. 1 except for ⁹⁰Zr. The very detailed experimental data are from a recent experiment by Wakasa et al. [60].

Figure 5: Relative errors in the spin-orbit splitting (calculated from the intrinsic single-particle energies) for the forces, nuclei, and states indicated. Only splittings between states which are both above or both below the Fermi surface are included. Other states are affected by core polarization and cannot be safely described by the mean field [7,8]. The forces SLy5-SkO are ordered according to their values for g₀' (see Fig. 3). SGII-u and SkM^*-u are two recent forces with modified spin-orbit interactions tailored for future use in GT resonance studies [62].

In ¹²⁴Sn, however, this simple picture does not hold, as Fig. 2 shows. The resonance energies are similar (and close to the experimental value) for SkP, SLy5, SkO, and SkO' forces with very different values of g₀', while SGII and SLy4 push the resonance energy too high. Only the amount of the low-lying strength seems to scale with g₀'. It is interesting, though, that the related forces SLy4 and SLy5 (which predict very similar single-particle spectra, but have quite different GT residual interactions) agree with the schematic model in that SLy4, with larger g₀', puts the GT resonance at a higher excitation energy.

It is clear that the scaling predicted by the schematic model is too simple, and Fig. 3 demonstrates this clearly. There we show the calculated strengths $B_{\rm res}$ in the GT resonances relative to the sum-rule value $B_{\rm tot}=3(N-Z)$, and the calculated GT resonance energies $E_{\rm calc}$ relative to the experimental values $E_{\rm expt}$. [For ⁹⁰Zr, ¹¹²Sn, ¹²⁴Sn, and ²⁰⁸Pb we used $E_{\rm expt} = 9.4$MeV, 8.9MeV, 13.7MeV, and 15.5MeV, respectively [46]. Note that the calculated resonance energy depends on a prescription (see [11]) not strictly dictated by the QRPA.] The scatter near $g_0' \approx 0.9$, in both the resonance energy and in the amount of low-lying strength, shows that other combinations of parameters in the residual interaction besides g₀' affect the GT distribution. This is not entirely surprising given the complexity of finite nuclei and of the interaction (14). In Sect. 4.3 we quantify these other important combinations and discuss their effects.

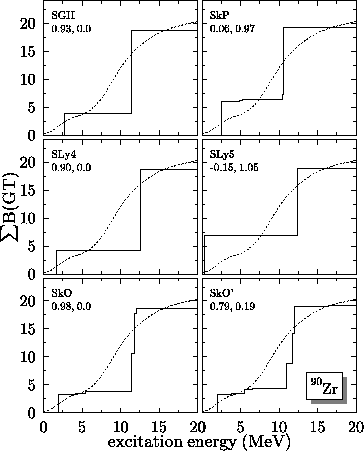
But another factor, this one determined by the time-even part of the Skyrme functional, affects the GT distribution: the underlying single-particle spectrum. Since GT transitions are especially sensitive to proton spin-orbit splittings, small changes in the time-even part of the force can, in principle, move the GT resonance considerably. Sensitivity to the spin-orbit splitting is particularly obvious in ⁹⁰Zr, where detailed information has been obtained from a recent experiment by Wakasa et al. [60]. Unlike in ¹²⁴Sn and ²⁰⁸Pb, which respond to a GT excitation in a collective way, the ⁹⁰Zr GT spectrum is dominated by two single-particle transitions, from the neutron 1g_9/2 state to the proton 1g_9/2 and 1g_7/2 states. The difference between the locations of the two peaks in the GT spectrum is the sum of the proton 1g spin-orbit splitting and a contribution from the residual interaction (which can be expected to increase the difference). As Fig. 4 shows, all interactions, whatever their value for g₀', overestimate this difference; the resonance energy is always too large, even when the residual interaction is switched off completely.

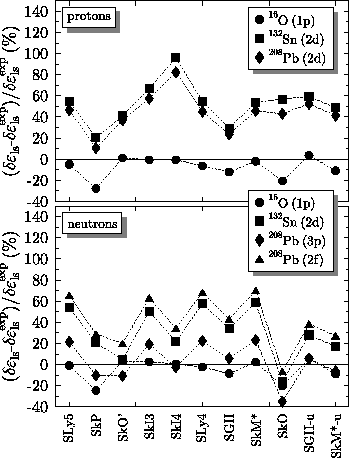
Most Skyrme interactions give spin-orbit splittings in heavy nuclei that are too large [61]. We can therefore expect errors in their predicted GT strength distributions [45,47]. Figure 5 shows errors in the predicted spin-orbit energies for the same forces as in Fig. 3. Interactions such as SkI3, SkI4, or SLy4 that overestimate the proton spin-orbit splittings give the largest resonance energies (and tend to overestimate them). The best interaction, in view of the combined information from Figs. 3 and 5, appears to be SkO'. Therefore, below, we use its time-even energy functional for further exploration of the time-odd terms.

We have included some new forces in Fig. 5; in a recent paper [62], Sagawa et al. attempt to improve the spin-orbit interaction for the standard Skyrme forces SIII, SkM^*, and SGII, aiming at better GT-response predictions. They generalize the spin-orbit interaction through the condition $C_0^{\nabla J} = - C_1^{\nabla J}$ and include the $\stackrel{\leftrightarrow}{J}^2$ term with a coupling given by Eq. (34). Although the modified forces SkM^*-u, and SGII-u give slightly better descriptions of GT resonances than the original interactions, they generate unacceptable errors in total binding energies and do not substantially improve the overall description of single-particle spectra in ²⁰⁸Pb.

A few remarks are in order before proceeding: (i) The spin-orbit splittings shown in Fig. 5 are calculated from intrinsic single-particle energies. Since experimental data are obtained from binding-energy differences between even-even and adjacent odd-mass nuclei, core polarization induced by the unpaired nucleon, which depends partly on time-odd channels of the interaction [7,8], alters single-particle energies. The effect is largest in small nuclei (of the order of 20 % in ¹⁶O), decreasing rapidly with mass number [8]. (ii) GT distributions are also affected by the particle-particle channel of the effective interaction, but mainly at low energies. The GT resonance is not materially altered [11], so we can safely neglect the particle-particle interaction here.