


Next: GT strength distributions from
Up: Giant Gamow-Teller resonances
Previous: Giant Gamow-Teller resonances
Non-self-consistent calculations often use the residual
Landau-Migdal interaction in the spin-isospin channel:
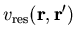 |
| |
= |
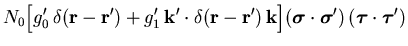 |
(13) |
where N0 is a normalization factor [see Eq. (69)] and
 and
and  are defined in Appendix 8.
In most applications, only the s-wave interaction with strength g0'
is used, and the matrix elements of the force are not antisymmetrized.
The underlying single-particle spectra are usually taken from
a parameterized potential, e.g., the Woods-Saxon potential.
Typical values for g0', obtained from fits to GT-resonance
systematics, are
are defined in Appendix 8.
In most applications, only the s-wave interaction with strength g0'
is used, and the matrix elements of the force are not antisymmetrized.
The underlying single-particle spectra are usually taken from
a parameterized potential, e.g., the Woods-Saxon potential.
Typical values for g0', obtained from fits to GT-resonance
systematics, are
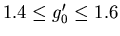 [45,46,47]. (See Ref. [48] for an early
compilation of data.) Sometimes this approach is formulated in terms
of the residual interaction between antisymmetrized states. The results
are similar, e.g., g0' = 1.54 in the double-
[45,46,47]. (See Ref. [48] for an early
compilation of data.) Sometimes this approach is formulated in terms
of the residual interaction between antisymmetrized states. The results
are similar, e.g., g0' = 1.54 in the double-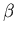 -decay
calculations by Engel et al. [49]. More complicated residual
interactions, like boson-exchange potentials, have been used as well;
see, e.g., Refs. [50,51,52]. Borzov et al. use
a renormalized one-pion exchange potential in connection with a
-decay
calculations by Engel et al. [49]. More complicated residual
interactions, like boson-exchange potentials, have been used as well;
see, e.g., Refs. [50,51,52]. Borzov et al. use
a renormalized one-pion exchange potential in connection with a
 Landau-Migdal interaction of type
(13) [53].
Landau-Migdal interaction of type
(13) [53].
A much simpler residual interaction in the GT channel is
a separable (or ``schematic") interaction,
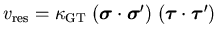 ,
where the strength
,
where the strength
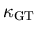 has to be a function of A. This interaction
is widely used in global calculations of nuclear
has to be a function of A. This interaction
is widely used in global calculations of nuclear 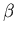 -decay
[54,55]. Sarriguren et al. [56]
use it for a description of the GT resonances in deformed
nuclei with quasiparticle energies obtained from self-consistent
HF+BCS calculations. They estimate
-decay
[54,55]. Sarriguren et al. [56]
use it for a description of the GT resonances in deformed
nuclei with quasiparticle energies obtained from self-consistent
HF+BCS calculations. They estimate
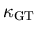 from the Landau
parameters of their Skyrme interaction. (The same prescription is used
in their calculations of M1 resonances [57].)
But however useful this approach may be from a technical point of
view, it is not self-consistent. Nor is it equivalent to using the
original residual Skyrme interaction; see, e.g., the
discussion in [46].
from the Landau
parameters of their Skyrme interaction. (The same prescription is used
in their calculations of M1 resonances [57].)
But however useful this approach may be from a technical point of
view, it is not self-consistent. Nor is it equivalent to using the
original residual Skyrme interaction; see, e.g., the
discussion in [46].
A truly self-consistent calculation, by contrast, should interpret
the QRPA as the small-amplitude limit of time-dependent HFB theory.
The Skyrme energy functional used in the HFB should then determine
the residual interaction between unsymmetrized states in the QRPA:
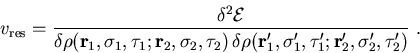 |
(14) |
The actual form of the residual interaction that contributes to the
QRPA matrix elements of 1+ states is outlined in Appendix
12.
Table 1:
Landau parameters for various Skyrme interactions from relations
(34) and the Gogny forces D1 and D1s.
Missing entries are zero by construction.
| Force |
g0 |
g1 |
g2 |
g0' |
g1' |
g2' |
|
SkM* |
0.33 |
|
|
0.94 |
|
|
| SGII |
0.62 |
|
|
0.93 |
|
|
| SkP |
-0.23 |
-0.18 |
|
0.06 |
0.97 |
|
| SkI3 |
1.89 |
|
|
0.85 |
|
|
| SkI4 |
1.77 |
|
|
0.88 |
|
|
| SLy4 |
1.39 |
|
|
0.90 |
|
|
| SLy5 |
1.14 |
0.24 |
|
-0.15 |
1.05 |
|
| SLy6 |
1.41 |
|
|
0.90 |
|
|
| SLy7 |
0.94 |
0.47 |
|
0.02 |
0.88 |
|
| SkO |
0.48 |
|
|
0.98 |
|
|
| SkO' |
-1.61 |
2.16 |
|
0.79 |
0.19 |
|
| SkX |
-0.63 |
0.18 |
|
0.51 |
0.53 |
|
|
D1 |
0.47 |
0.06 |
0.12 |
0.60 |
0.34 |
0.08 |
| D1s |
0.48 |
-0.19 |
0.25 |
0.62 |
0.62 |
-0.04 |



Next: GT strength distributions from
Up: Giant Gamow-Teller resonances
Previous: Giant Gamow-Teller resonances
Jacek Dobaczewski
2002-03-15
![]() ,
where the strength
,
where the strength
![]() has to be a function of A. This interaction
is widely used in global calculations of nuclear
has to be a function of A. This interaction
is widely used in global calculations of nuclear ![]() -decay
[54,55]. Sarriguren et al. [56]
use it for a description of the GT resonances in deformed
nuclei with quasiparticle energies obtained from self-consistent
HF+BCS calculations. They estimate
-decay
[54,55]. Sarriguren et al. [56]
use it for a description of the GT resonances in deformed
nuclei with quasiparticle energies obtained from self-consistent
HF+BCS calculations. They estimate
![]() from the Landau
parameters of their Skyrme interaction. (The same prescription is used
in their calculations of M1 resonances [57].)
But however useful this approach may be from a technical point of
view, it is not self-consistent. Nor is it equivalent to using the
original residual Skyrme interaction; see, e.g., the
discussion in [46].
from the Landau
parameters of their Skyrme interaction. (The same prescription is used
in their calculations of M1 resonances [57].)
But however useful this approach may be from a technical point of
view, it is not self-consistent. Nor is it equivalent to using the
original residual Skyrme interaction; see, e.g., the
discussion in [46].