MP parametrization of EEG structures

One of the first applications of MP in EEG analysis was detection and parametrization of sleep spindles--structures present in sleep EEG recordings [3][4]. The definition given in a classical reference [7] states: "The presence of sleep spindle should not be defined unless it is at least 0.5 sec. duration, i.e. one should be able to count 6 or 7 distinct waves within the half-second period. (...) The term should be used only to describe activity between 12 and 14 cps." Although intended for standardization of visual detection, the above definition is almost directly translatable into the time-frequency parameters of MP atoms fitted to analyzed EEG. Since the shape of sleep spindles is quite similar to Gabor functions, we can basically assume a one-to-one relationship between sleep spindles and atoms fitted to EEG, conforming to the above definition. This yields an automatic parametrization of structures conforming to selected time-frequency criteria. Details of this procedure, as well as examples of parametrization of other EEG structures, are given e.g. in [4] and [8].

The middle and lower plots of Figure 1 present histograms of frequencies of sleep spindles as detected using the above procedure in an overnight EEG recording. MP decomposition was performed on consecutive 20-sec epochs of EEG from sleep stage II (above 3 hours), 12-bit ADC, and sampling frequency 128 Hz.

Figure 1: Histograms of frequencies of sleep spindles from an overnight EEG recording, selected from MP parametrization in a dyadic (middle plot, section I-B) dictionary and stochastic Gabor dictionaries (lower plot, section II). The upper plot is a histogram of frequencies of atoms available for decomposition in the dyadic dictionary (for the frequencies of interest). The dark bars represent scales 64-256 chosen for sleep spindles, light gray is used for the rest of scales.

The histogram in the middle plot is based on MP decomposition in a dyadic dictionary (section I-B) . Its most striking feature is a regular, repeating pattern superimposed on the overall trend of concentration spindles around 13 Hz. This regular structure is an artifact of the analysis method.

The time-frequency centers of the atoms from a dyadic dictionary form a regular lattice. The upper plot of Figure 1 presents a histogram of frequencies of all the atoms from a dyadic dictionary, within the frequency range of interest. Its pattern can be recognized in the middle plot. A higher density of atoms available for decomposition at certain frequencies ``attracts'' results of the nonlinear MP procedure, and more waveforms are fitted at these frequencies.

The histogram in the lower plot of Figure 1 is constructed from a statistically unbiased MP representation, which was obtained by decomposition of the same EEG data as in the middle plot using stochastic dictionaries. Their size was equal to the size of the dyadic dictionary used to compute the middle plot's data ( 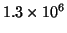$1.3\times 10^6$ waveforms). We observe the absence of the artifactual maxima, conforming to physiological expectations.

Figure 2: Illustration of the effect from Figure 1 on simulated data. 200 realizations of 128-points white noise process were subjected to MP decomposition in dyadic (middle plot) and stochastic (bottom) dictionaries. The middle and lower plots present histograms of frequencies of all the structures fitted by MP. The upper plot is a histogram of frequencies of all the time-frequency atoms present in the dyadic dictionary used for the decomposition presented in the middle plot.

The analogous effect is illustrated in Figure 2, where frequencies of atoms fitted to white noise reveal the structure of the dyadic dictionary (middle plot) or expected flat characteristics when obtained by MP with stochastic dictionaries (bottom).