

Next: Conclusion
Up: Results
Previous: MP parametrization of EEG
Averaging time-frequency representations of one signal in several stochastic dictionaries
The proposed idea can be also applied to a single data epoch. Let's consider a signal simulated as
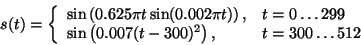 |
(7) |
The upper plot of figure 3 presents the result of decomposition of this signal over a large dictionary
(
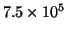 Gabor functions). In spite of the high resolution of this decomposition, the
changing frequency is represented by a series of structures since all the dictionary's functions have constant frequency.
The middle plot of Figure 3 shows an average of 50 time-frequency representations constructed from
decompositions over different realizations of small (
Gabor functions). In spite of the high resolution of this decomposition, the
changing frequency is represented by a series of structures since all the dictionary's functions have constant frequency.
The middle plot of Figure 3 shows an average of 50 time-frequency representations constructed from
decompositions over different realizations of small (
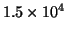 ) stochastic dictionaries. Their size was optimized
for this particular signal, and the number of averaged decompositions was chosen to make the computational costs
of both representations equal (compare section II).
The plot in the middle panel corresponds better to Equation 7. However, it is constructed from
50 times more waveforms than the upper plot, so the underlying parametrization is not compact.
) stochastic dictionaries. Their size was optimized
for this particular signal, and the number of averaged decompositions was chosen to make the computational costs
of both representations equal (compare section II).
The plot in the middle panel corresponds better to Equation 7. However, it is constructed from
50 times more waveforms than the upper plot, so the underlying parametrization is not compact.
Figure 3:
Energy density (
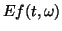 , eq. (5), proportional to shades of gray) of a simulated signal
(bottom plot), calculated from single MP decomposition over a dictionary containing
, eq. (5), proportional to shades of gray) of a simulated signal
(bottom plot), calculated from single MP decomposition over a dictionary containing
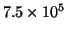 waveforms (top)
and averaged over 50 decompositions in different realizations of stochastic dictionaries,
containing
waveforms (top)
and averaged over 50 decompositions in different realizations of stochastic dictionaries,
containing
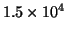 atoms each (middle plot).
atoms each (middle plot).
![\includegraphics[width=\columnwidth]{figures/fig3.eps}](img53.png) |


Next: Conclusion
Up: Results
Previous: MP parametrization of EEG
Piotr J. Durka
2001-03-23
![\includegraphics[width=\columnwidth]{figures/fig3.eps}](img53.png)