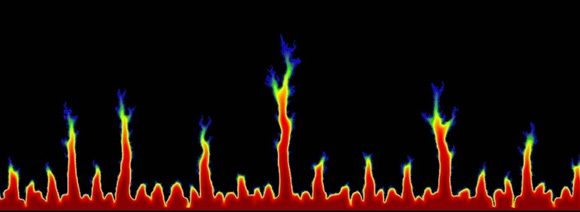
Nonequilibrium growth processes
Dissolution in fractured rocks
I am interested in the theoretical and numerical analysis of interface dynamics in nonequilibrium growth processes. A remarkable example of such a process is the dissolution of porous or fractured rock, such as the limestone dissolution by carbon dioxide-enriched water which leads to the formation of spectacular cave and karst features.
The evolving topography of the pore space depends strongly on the fluid flow and mineral dissolution rates. Remarkably, there exists a wide parameter range in which the positive feedback between fluid transport and mineral dissolution leads to the spontaneous formation of pronounced channels, frequently referred to as "wormholes". As dissolution proceeds the growing channels interact, competing for the available flow, and eventually the growth of the shorter ones cease. This leads to self-similar patterns of growth, with the flow becoming concentrated in fewer active channels. The understanding of dissolution dynamics is not only basic for a proper description of cave formation processes, but also important in a number of geochemical applications, such as CO2 sequestration and stimulation of petroleum reservoirs.
In recent years, together with Tony Ladd from University of Florida, we have constructed a detailed, three-dimensional numerical model of a dissolving fractured rock, capable of simulating relatively large fractures. Additionaly, a number of simpler models were constructed, aimed to capture the fundamental physics of the channel-channel interaction process. In particular, since the pressure field in the rock matrix obeys the Laplace equation, the competition between the channels may be described in terms of a Laplacian growth model and solved using conformal mapping techniques.
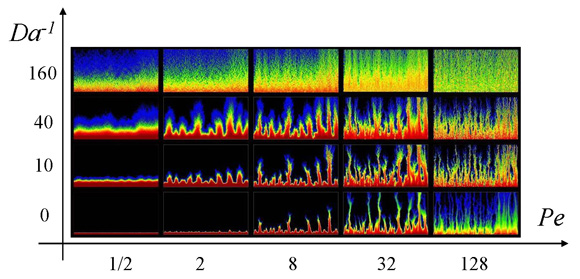
Dissolution patterns for different Péclet and Damköhler numbers. The Péclet number measures the relative magnitude of convective and diffusive transport of the solute, Pe = v < h > / D, where v ia a characteristic fluid velocity, < h > is the mean aperture and D is the solute diffusion coefficient. The Damköhler number, Da = k/v, relates the surface reaction rate to convective transport.
movies:
rough_fracture.avi
Formation and evolution of the channels during dissolution of a rough fracture, with relative roughness f=σ/
smooth_fracture.avi
The same for a smooth fracture with f=0.05
In collaboration with
- Tony Ladd (University of Florida)
- Agnieszka Budek, Paweł Kondratiuk, Florian Osselin, Karine Petrus, Michał Pecelerowicz, Hanna Trędak (University of Warsaw)
Relevant publications
- F. Osselin, P. Kondratiuk, A Budek, O. Cybulski, P. Garstecki, P. Szymczak Microfluidic observation of the onset of reactive infiltration instability in an analog fracture, Geophys. Res. Lett., 43, 6907-6915, 2016 [pdf]
- K. Petrus, P. Szymczak, Influence of layering on the formation and growth of solution pipes, Front. Phys., 3, 92, 2016 [pdf]
- Y. Cohen, O. Devauchelle, H. F. Seybold, R. S. Yi, P. Szymczak, D. Rothman, Path selection in the growth of rivers, Proc. Natl. Acad. Sci. USA, 112 , 14132-14137, 2015 [pdf] [press coverage]
- V. K. Upadhyay, P. Szymczak, A. J. C. Ladd, Initial conditions or emergence; what determines dissolution patterns in rough fractures?, J. Geophys. Res. Solid Earth, 120, 6102-6121, 2015 [pdf] [movie1] [movie2] [movie3] [movie4] [movie5]
- A. Budek, P. Garstecki, A. Samborski, and P. Szymczak, Thin-finger growth and droplet pinch-off in miscible and immiscible displacements in a periodic network of microfluidic channels, Phys. Fluids., 27, 112109, 2015 [pdf]
- P. Kondratiuk, P. Szymczak, Steadily translating parabolic dissolution fingers, SIAM J. Appl. Math., 75, 2193--2213, 2015 [pdf]
- P. Kondratiuk, H. Tredak, A.J.C. Ladd, P. Szymczak, Synchronization of dissolution and precipitation fronts during infiltration-driven replacement in porous rocks, Geophys. Res. Lett. 44, 2244-2252, 2015 [pdf]
- M. Pecelerowicz, A. Budek, P. Szymczak, Effective description of the interaction between anisotropic viscous fingers, EPL, 108, 14001, 2014 (Editor's choice) [pdf]
- M. Pecelerowicz, A. Budek, P. Szymczak, Competition between anisotropic viscous fingers, Eur. Phys. J. Special Topics, 223, 1895-1906, 2014 [pdf]
- P. Szymczak, A. J. C. Ladd, Reactive-infiltration instabilities in rocks. Part II: Dissolution of a porous matrix., J. Fluid Mech., 738, 591-630, 2014 [pdf]
- P. Szymczak, A. J. C. Ladd, Interacting length scales in the reactive-infiltration instability, Geophys. Res. Lett., 40, 3036-3041, 2013 [pdf] [supplementary]
- A. Budek, P. Szymczak, Network models of dissolution of porous media, Phys. Rev. E, 86, 056318, 2012 [pdf]
- P. Szymczak, A. J. C. Ladd, Reactive-infiltration instabilities in rocks. Fracture dissolution., J. Fluid Mech., 702, 239-264, 2012 [pdf]
- P. Szymczak, A. J. C. Ladd, Instabilities in the dissolution of a porous matrix, Geophys. Res. Lett., 38, L07403, 2011 [pdf]
- P. Szymczak, A. J. C. Ladd, The initial stages of cave formation: Beyond the one-dimensional paradigm, Earth Planet. Sci. Lett., 301, 424-432, 2011 [pdf] [movie] Press Coverage: [Science Editor's Choice] [Science News] [Wired]
- P. Szymczak, A. J. C. Ladd, Wormhole formation in dissolving fractures, J. Geophys. Res., 114, B06203, 2009 [pdf]
- P. Szymczak, A. J. C. Ladd, Comment on: "From pore scale to wellbore scale: Impact of geometry on wormhole growth in carbonate acidization" by C. E. Cohen et al., Chem. Eng. Sci., 64, 3029, 2009 [pdf]
- T. Gubiec, P. Szymczak, Fingered growth in channel geometry: A Loewner equation approach , Phys. Rev. E, 77, 041602, 2008 [pdf]
- P. Szymczak, A. J. C. Ladd, A network model of channel competition in fracture dissolution, Geophys. Res. Lett., 33, L05401, 2006 [pdf]
- P. Szymczak, A. J. C. Ladd, Microscopic simulations of fracture dissolution, Geophys. Res. Lett., 31, L23606, 2004 [pdf]
- P. Szymczak, A. J. C. Ladd, Stochastic boundary conditions to the convection-diffusion equation including chemical reactions at solid surfaces, Phys. Rev. E, 69, 036704, 2004 [pdf]
- P. Szymczak, A. J. C. Ladd, Boundary conditions for stochastic solutions of the convection-diffusion equation, Phys. Rev. E, 68, 036704, 2003 [pdf]