In the following page you'll find materials for course Advanced Hydrodynamics taught at Warsaw University Physics Department in 2021.
This course follows problem-based learning and materials are divided into modules related to specific experiments involving flow.
In many cases we'll use Mathematica to quickly test different models during discussions. Slightly cleaned up notebooks will be uploaded after meets
Mathematica licences can be obtained here.
Notes from the lectures will be posted here, together with various other sources.
Following prompt was given during International Young Physicist Torunament:
A ‘vacuum bazooka’ can be built with a simple plastic pipe, a light projectile, and a vacuum cleaner. Build such a device and maximise the muzzle velocity.
You can find an example of such device in this YouTube video or this video.
How would one optimize such device? How does the bullet interact with the flow? What physical phenomena limit muzzle velocity?
Background reading:
A Mathematica notebook (stub) for optimizing bazookas: link.
Following prompt was given during International Young Physicist Torunament:
In the Leidenfrost effect, a water drop placed on a hot surface can survive for minutes. Under certain circumstances, such a drop develops oscillating star shapes. Induce different oscillatory modes and investigate them.
It's quite easy to recreate in your home (try it!), but you can also look at a slow motion vide here for example.
Why do they vibrate? What is the role of the Leidenfrost effect? How to find the period of oscillation?
Background reading:
More depth:
Questions to the Phys.Rev.Fluids paper:
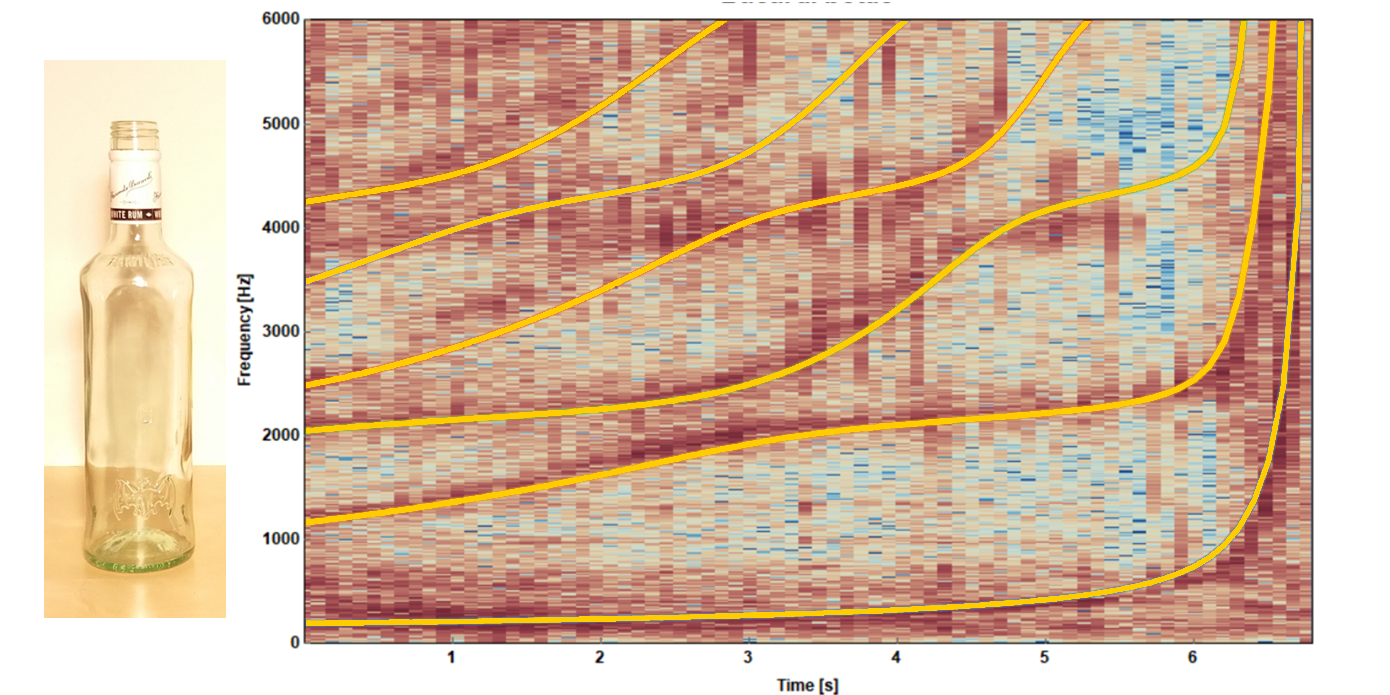
Following prompt was given during International Young Physicist Torunament:
When a vertical water jet enters a bottle, sound may be produced, and, as the bottle is filled up, the properties of the sound may change. How does the bottle size and shape influence the phenomenon?
If you need a video reference try here.
Compare the value of dominant frequency observed to acoustic resonance of half-open cyllinder. What did you find?
Following prompt was given during International Young Physicist Torunament:
When a smooth column of water hits a horizontal plane, it flows out radially. At some radius, its height suddenly rises. Investigate the nature of the phenomenon. What happens if a liquid more viscous than water is used?
You can find demonstration of a hydraulic jump in a clear plastic setup here.
Use a flat plane (such as cutting board, most plates are too concave) below a faucet to observe hydraulic jump a different velocities of the impinging jet. What can you say about the radius of the jump?
Background reading:
More depth:
Questions to the J.Fluid.Mech. paper:
Produce a stable laminar jet of flowing water by opening the kitchen tap (or otherwise). After travelling some length, an instability develops and the jet breaks up into droplets. Investigate this phenomenon. Explore the shape of the falling jet, the breakup mechanism and the evolution of the stream. An analogous phenomenon happens with a liquid sheet, e.g. one flowing out from a square-shaped box over the side. Discuss the similarities and differences.
For the observations, you can use plotting paper and/or a mobile phone with a camera (and possibly a slow motion video mode).
Pay particular attention to include the following parts in your mini-paper:
TBA